Finite State Automata DFA Dan NFA

Automata - Apa itu?

Istilah "Automata" berasal dari kata Yunani "αὐτόματα" yang berarti "bertindak sendiri". Automaton (Automata dalam jamak) adalah perangkat komputasi self-propelled abstrak yang mengikuti urutan operasi yang telah ditentukan secara otomatis.

Automaton dengan sejumlah negara terbatas disebut Finite Automaton (FA) atau Finite State Machine (FSM).

Definisi formal tentang Automaton Terbatas

Otomat dapat diwakili oleh 5-tupel (Q, ∑, δ, q 0 , F), di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol yang terbatas, yang disebut alfabet automaton.
• δ adalah fungsi transisi.
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).
• F adalah seperangkat status akhir / status Q (F ⊆ Q).

Terminologi Terkait

Alfabet

• Definisi - Alfabet adalah seperangkat simbol yang terbatas.
• Contoh - β = {a, b, c, d} adalah seperangkat alfabet tempat 'a', 'b', 'c', dan 'd' adalah simbol .

Tali

• Definisi - String adalah urutan simbol terbatas yang diambil dari.
• Contoh - 'cabcad' adalah string yang valid pada set alfabet β = {a, b, c, d}

Panjang sebuah String

• Definisi - Ini adalah jumlah simbol yang ada dalam string. (Dilambangkan oleh | S | ).
• Contoh -
  • Jika S = 'cabcad', | S | = 6
  • Jika | S | = 0, ini disebut string kosong (dilambangkan dengan λ atau ε )

Bintang Kleene

• Definisi - Bintang Kleene, ∑ * , adalah operator unary pada serangkaian simbol atau string,, yang memberikan himpunan tak terbatas dari semua string yang mungkin dari semua panjang yang mungkin di atas ∑ termasuk λ .
• Representasi - ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. di mana ∑ p adalah himpunan semua string yang mungkin panjang p.
• Contoh - Jika ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}

Penutupan Kleene / Plus

• Definisi - Himpunan ∑ + adalah himpunan tak terbatas dari semua string yang mungkin dari semua panjang yang mungkin di atas ∑ tidak termasuk λ.
• Representasi - ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
  ∑ + = ∑ * - {λ}
• Contoh - Jika ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}

Bahasa

• Definisi - Suatu bahasa adalah himpunan bagian dari * untuk beberapa alfabet. Itu bisa terbatas atau tidak terbatas.
• Contoh - Jika bahasa mengambil semua string yang mungkin dengan panjang 2 lebih ∑ = {a, b}, maka L = {ab, aa, ba, bb}

Deterministic Finite Automaton

Hingga Otomat dapat diklasifikasikan menjadi dua jenis -

• Deterministic Finite Automaton (DFA)
• Finite Automaton Non-deterministik (NDFA / NFA)

Deterministic Finite Automaton (DFA)

Dalam DFA, untuk setiap simbol input, seseorang dapat menentukan status kemana mesin akan bergerak. Oleh karena itu, itu disebut Deterministic Automaton . Karena memiliki sejumlah negara terbatas, mesin ini disebut Deterministic Finite Machine atau Deterministic Finite Automaton.

Definisi Resmi DFA

DFA dapat diwakili oleh 5-tupel (Q, ∑, δ, q 0 , F) di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol terbatas yang disebut alfabet.
• δ adalah fungsi transisi di mana δ: Q × ∑ → Q
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).
• F adalah seperangkat status akhir / status Q (F ⊆ Q).

Representasi Grafis dari DFA

DFA diwakili oleh digraf yang disebut diagram keadaan .

• Verteks mewakili negara.
• Busur berlabel alfabet input menunjukkan transisi.
• Keadaan awal dilambangkan dengan satu busur masuk yang kosong.
• Keadaan akhir ditunjukkan oleh lingkaran ganda.

Contoh

Biarkan otomat terbatas deterministik menjadi →

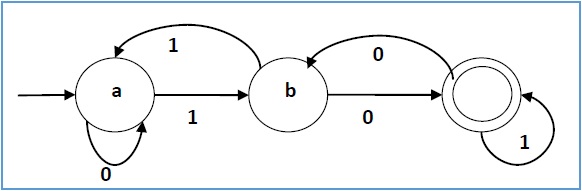
• Q = {a, b, c},
• ∑ = {0, 1},
• q 0 = {a},
• F = {c}, dan

Fungsi transisi δ seperti yang ditunjukkan oleh tabel berikut -

Keadaan saat ini	Status Selanjutnya untuk Input 0	Status Selanjutnya untuk Input 1
Sebuah	Sebuah	b
b	c	Sebuah
c	b	c

Representasi grafisnya adalah sebagai berikut -

Non-deterministic Finite Automaton

Dalam NDFA, untuk simbol input tertentu, mesin dapat berpindah ke kombinasi status apa pun di dalam mesin. Dengan kata lain, kondisi pasti tempat mesin bergerak tidak dapat ditentukan. Oleh karena itu, itu disebut Non-deterministic Automaton . Karena memiliki jumlah negara hingga, mesin ini disebut Mesin Hingga Non-deterministik atau Non-deterministic Finite Automaton .

Definisi Resmi suatu NDFA

NDFA dapat diwakili oleh 5-tupel (Q,, δ, q 0 , F) di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol terbatas yang disebut huruf.
• δ adalah fungsi transisi di mana δ: Q × ∑ → 2 Q
  (Di sini set daya Q (2 Q ) telah diambil karena dalam kasus NDFA, dari suatu keadaan, transisi dapat terjadi pada kombinasi dari keadaan Q)
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).
• F adalah seperangkat status akhir / status Q (F ⊆ Q).

Representasi Grafis dari NDFA: (sama seperti DFA)

NDFA diwakili oleh digraf yang disebut diagram keadaan.

• Verteks mewakili negara.
• Busur berlabel alfabet input menunjukkan transisi.
• Keadaan awal dilambangkan dengan satu busur masuk yang kosong.
• Keadaan akhir ditunjukkan oleh lingkaran ganda.

Contoh

Biarkan otomat hingga non-deterministik menjadi →

• Q = {a, b, c}
• Β = {0, 1}
• q 0 = {a}
• F = {c}

Fungsi transisi δ seperti yang ditunjukkan di bawah ini -

Keadaan saat ini	Status Selanjutnya untuk Input 0	Status Selanjutnya untuk Input 1
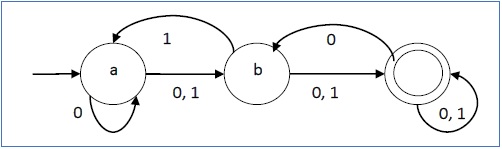
Sebuah	a, b	b
b	c	a, c
c	b, c	c

Representasi grafisnya adalah sebagai berikut -

DFA vs NDFA

Tabel berikut mencantumkan perbedaan antara DFA dan NDFA.

DFA	NDFA
Transisi dari keadaan adalah ke keadaan berikutnya tunggal khusus untuk setiap simbol input. Karena itu disebut deterministik .	Transisi dari status dapat ke beberapa status berikutnya untuk setiap simbol input. Karena itu disebut non-deterministik .
Transisi string kosong tidak terlihat di DFA.	NDFA mengizinkan transisi string kosong.
Mengulangi diizinkan dalam DFA	Di NDFA, mundur tidak selalu mungkin.
Membutuhkan lebih banyak ruang.	Membutuhkan lebih sedikit ruang.
Suatu string diterima oleh DFA, jika transit ke keadaan akhir.	Sebuah string diterima oleh NDFA, jika setidaknya satu dari semua transisi yang mungkin berakhir dalam keadaan akhir.

Akseptor, Klasifikasi, dan Transduser

Akseptor (Pengenal)

Otomat yang menghitung fungsi Boolean disebut akseptor . Semua status akseptor menerima atau menolak input yang diberikan padanya.

Penggolong

Klasifikasi memiliki lebih dari dua status akhir dan memberikan output tunggal ketika berakhir.

Transduser

Otomat yang menghasilkan output berdasarkan input saat ini dan / atau keadaan sebelumnya disebut transduser . Transduser dapat terdiri dari dua jenis -

• Mesin Mealy - Output tergantung pada kondisi saat ini dan input saat ini.
• Moore Machine - Output hanya tergantung pada kondisi saat ini.

Penerimaan oleh DFA dan NDFA

Sebuah string diterima oleh DFA / NDFA jika DFA / NDFA dimulai dari keadaan awal berakhir pada keadaan penerima (salah satu dari status akhir) setelah membaca string sepenuhnya.

String S diterima oleh DFA / NDFA (Q,, δ, q 0 , F), iff

δ * (q 0 , S) ∈ F

Bahasa L yang diterima oleh DFA / NDFA adalah

{S | S ∈ ∑ * dan δ * (q 0 , S) ∈ F}

String S ′ tidak diterima oleh DFA / NDFA (Q,, δ, q 0 , F), iff

δ * (q 0 , S ′) ∉ F

Bahasa L ′ tidak diterima oleh DFA / NDFA (Pelengkap bahasa yang diterima L) adalah

{S | S ∈ ∑ * dan δ * (q 0 , S) ∉ F}

Contoh

Mari kita perhatikan DFA yang ditunjukkan pada Gambar 1.3. Dari DFA, string yang dapat diterima dapat diturunkan.

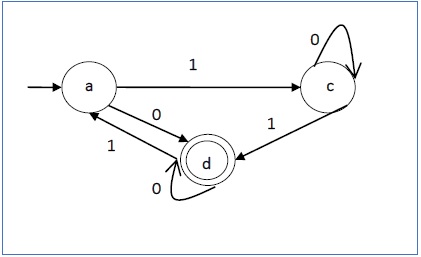
String diterima oleh DFA di atas: {0, 00, 11, 010, 101, ...........}

String tidak diterima oleh DFA di atas: {1, 011, 111, ........}

Konversi NDFA ke DFA

Pernyataan masalah

Misalkan X = (Q x , ∑, δ x , q 0 , F x ) menjadi NDFA yang menerima bahasa L (X). Kita harus merancang DFA Y = (Qy,, δ y , q 0 , F y ) yang ekivalen sehingga L (Y) = L (X) . Prosedur berikut mengubah NDFA ke DFA yang setara -

Algoritma

Input - Sebuah NDFA

Output - DFA yang setara

Langkah 1 - Buat tabel negara dari NDFA yang diberikan.

Langkah 2 - Buat tabel keadaan kosong di bawah abjad input yang mungkin untuk DFA yang setara.

Langkah 3 - Tandai status awal DFA dengan q0 (Sama seperti NDFA).

Langkah 4 - Cari tahu kombinasi States {Q 0 , Q 1 , ..., Q n } untuk setiap alfabet input yang memungkinkan.

Langkah 5 - Setiap kali kita menghasilkan status DFA baru di bawah kolom alfabet masukan, kita harus menerapkan langkah 4 lagi, jika tidak, lanjutkan ke langkah 6.

Langkah 6 - Negara-negara bagian yang berisi negara bagian terakhir NDFA adalah negara bagian terakhir dari DFA yang setara.

Contoh

Mari kita perhatikan NDFA yang ditunjukkan pada gambar di bawah ini.

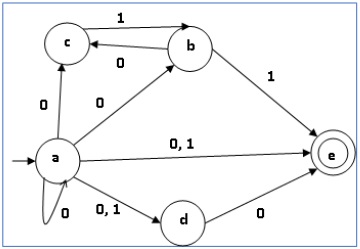
q	δ (q, 0)	δ (q, 1)
Sebuah	{a, b, c, d, e}	{d, e}
b	{c}	{e}
c	∅	{b}
d	{e}	∅
e	∅	∅

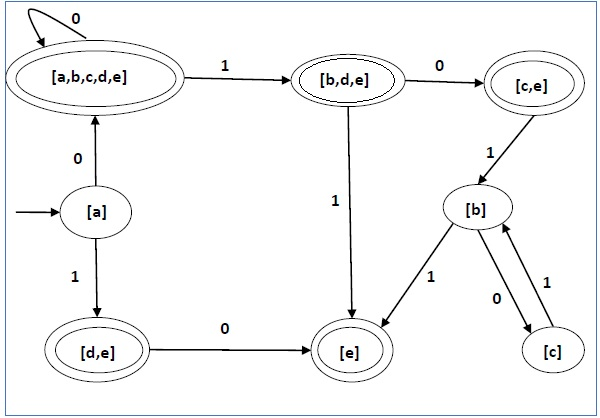
Dengan menggunakan algoritma di atas, kami menemukan DFA yang setara. Tabel status DFA ditunjukkan di bawah ini.

q	δ (q, 0)	δ (q, 1)
[Sebuah]	[a, b, c, d, e]	[d, e]
[a, b, c, d, e]	[a, b, c, d, e]	[b, d, e]
[d, e]	[e]	∅
[b, d, e]	[c, e]	[e]
[e]	∅	∅
[c, e]	∅	[b]
[b]	[c]	[e]
[c]	∅	[b]

Diagram keadaan DFA adalah sebagai berikut -

Minimalisasi DFA

Minimalisasi DFA menggunakan Teorema Myhill-Nerode

Algoritma

Input - DFA

Output - Meminimalkan DFA

Langkah 1 - Gambarlah tabel untuk semua pasangan negara (Q i , Q j ) belum tentu terhubung langsung [Semua awalnya tidak ditandai]

Langkah 2 - Pertimbangkan setiap pasangan negara (Q i , Q j ) di DFA di mana Q i ∈ F dan Q j ∉ F atau sebaliknya dan tandai mereka. [Di sini F adalah himpunan status akhir]

Langkah 3 - Ulangi langkah ini sampai kami tidak dapat menandai lagi menyatakan -

Jika ada pasangan yang tidak ditandai (Q i , Q j ), tandai jika pasangan {δ (Q i , A), δ (Q i , A)} ditandai untuk beberapa alfabet input.

Langkah 4 - Gabungkan semua pasangan yang tidak bertanda (Q i , Q j ) dan jadikan mereka satu status dalam DFA tereduksi.

Contoh

Mari kita gunakan Algoritma 2 untuk meminimalkan DFA yang ditunjukkan di bawah ini.

Langkah 1 - Kami menggambar tabel untuk semua pasangan negara.

	Sebuah	b	c	d	e	f
Sebuah
b
c
d
e
f

Langkah 2 - Kami menandai pasangan negara.

	Sebuah	b	c	d	e	f
Sebuah
b
c	✔	✔
d	✔	✔
e	✔	✔
f			✔	✔	✔

Langkah 3 - Kami akan mencoba untuk menandai pasangan negara, dengan tanda centang berwarna hijau, secara transitif. Jika kita memasukkan 1 untuk menyatakan 'a' dan 'f', maka masing-masing akan menyatakan 'c' dan 'f'. (c, f) sudah ditandai, maka kami akan menandai pasangan (a, f). Sekarang, kita input 1 untuk menyatakan 'b' dan 'f'; itu akan masing-masing menyatakan 'd' dan 'f'. (d, f) sudah ditandai, maka kami akan menandai pasangan (b, f).

	Sebuah	b	c	d	e	f
Sebuah
b
c	✔	✔
d	✔	✔
e	✔	✔
f	✔	✔	✔	✔	✔

Setelah langkah 3, kami mendapatkan kombinasi status {a, b} {c, d} {c, e} {d, e} yang tidak ditandai.

Kita dapat menggabungkan kembali {c, d} {c, e} {d, e} menjadi {c, d, e}

Karenanya kami mendapat dua status gabungan sebagai - {a, b} dan {c, d, e}

Jadi DFA yang diminimalkan akhir akan berisi tiga status {f}, {a, b} dan {c, d, e}

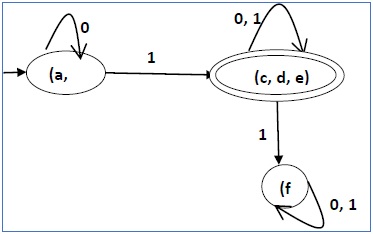
Minimalisasi DFA menggunakan Teorema Kesetaraan

Jika X dan Y adalah dua status dalam DFA, kita dapat menggabungkan kedua status ini menjadi {X, Y} jika keduanya tidak dapat dibedakan. Dua keadaan dapat dibedakan, jika setidaknya ada satu string S, sehingga salah satu dari δ (X, S) dan δ (Y, S) menerima dan yang lainnya tidak menerima. Oleh karena itu, DFA minimal jika dan hanya jika semua negara dapat dibedakan.

Algoritma 3

Langkah 1 - Semua status Q dibagi dalam dua partisi - status akhir dan status non-final dan dilambangkan dengan P 0 . Semua status dalam partisi setara dengan 0. Ambil penghitung k dan inisialisasi dengan 0.

Langkah 2 - Bertambah k dengan 1. Untuk setiap partisi dalam P k , bagi status dalam P k menjadi dua partisi jika k-dibedakan. Dua status dalam partisi X dan Y ini dapat dibedakan k jika ada input S sehingga δ (X, S) dan δ (Y, S) adalah (k-1) -distinguishable.

Langkah 3 - Jika P k ≠ P k-1 , ulangi Langkah 2, jika tidak pergi ke Langkah 4.

Langkah 4 - Gabungkan set ekuivalen ke k dan menjadikannya status baru dari DFA tereduksi.

Contoh

Mari kita pertimbangkan DFA berikut -

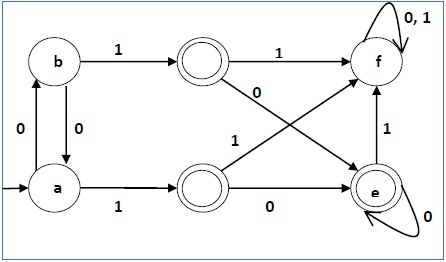
q	δ (q, 0)	δ (q, 1)
Sebuah	b	c
b	Sebuah	d
c	e	f
d	e	f
e	e	f
f	f	f

Mari kita terapkan algoritma di atas ke DFA di atas -

• P 0 = {(c, d, e), (a, b, f)}
• P 1 = {(c, d, e), (a, b), (f)}
• P 2 = {(c, d, e), (a, b), (f)}

Karenanya, P 1 = P 2 .

Ada tiga negara bagian dalam DFA yang dikurangi. Mengurangi DFA adalah sebagai berikut -

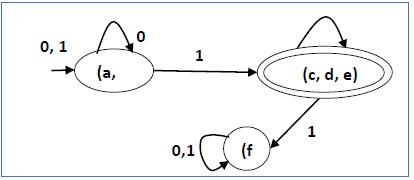
Q	δ (q, 0)	δ (q, 1)
(a, b)	(a, b)	(c, d, e)
(c, d, e)	(c, d, e)	(f)
(f)	(f)	(f)

Mesin Moore dan Mealy

Automata terbatas mungkin memiliki keluaran yang sesuai dengan setiap transisi. Ada dua jenis mesin negara terbatas yang menghasilkan output -

• Mesin Mealy
• Mesin Moore

Mesin Mealy

Mesin Mealy adalah FSM yang outputnya tergantung pada kondisi saat ini dan juga input saat ini.

Ini dapat dijelaskan dengan 6 tupel (Q, ∑, O, δ, X, q 0 ) di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol terbatas yang disebut alfabet input.
• O adalah seperangkat simbol terbatas yang disebut alfabet keluaran.
• δ adalah fungsi transisi input di mana δ: Q × ∑ → Q
• X adalah fungsi transisi keluaran di mana X: Q × ∑ → O
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).

Tabel keadaan Mesin Mealy ditunjukkan di bawah ini -

Kondisi sekarang	Keadaan selanjutnya
	input = 0		input = 1
	Negara	Keluaran	Negara	Keluaran
→ a	b	x 1	c	x 1
b	b	x 2	d	x 3
c	d	x 3	c	x 1
d	d	x 3	d	x 2

Diagram keadaan Mesin Mealy di atas adalah -

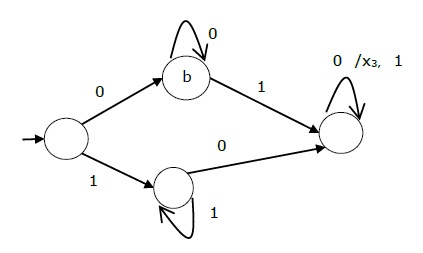
Mesin Moore

Mesin Moore adalah FSM yang outputnya hanya bergantung pada kondisi saat ini.

Mesin Moore dapat digambarkan dengan 6 tuple (Q, ∑, O, δ, X, q 0 ) di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol terbatas yang disebut alfabet input.
• O adalah seperangkat simbol terbatas yang disebut alfabet keluaran.
• δ adalah fungsi transisi input di mana δ: Q × ∑ → Q
• X adalah fungsi transisi output di mana X: Q → O
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).

Tabel keadaan Mesin Moore ditunjukkan di bawah ini -

Kondisi sekarang	Negara bagian selanjutnya		Keluaran
	Input = 0	Input = 1
→ a	b	c	x 2
b	b	d	x 1
c	c	d	x 2
d	d	d	x 3

Diagram keadaan Mesin Moore di atas adalah -

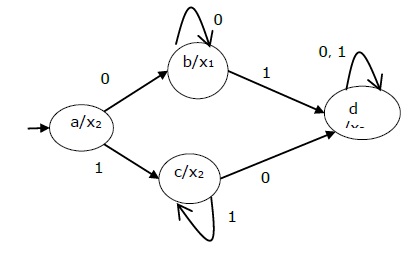
Mesin Mealy vs. Mesin Moore

Tabel berikut ini menyoroti poin-poin yang membedakan Mesin Mealy dari Mesin Moore.

Mesin Mealy	Mesin Moore
Output tergantung pada kondisi saat ini dan input saat ini	Output hanya tergantung pada kondisi saat ini.
Secara umum, ia memiliki lebih sedikit status daripada Moore Machine.	Secara umum, ia memiliki lebih banyak status daripada Mesin Mealy.
Nilai fungsi output adalah fungsi transisi dan perubahan, ketika logika input pada kondisi saat ini dilakukan.	Nilai fungsi output adalah fungsi dari kondisi saat ini dan perubahan di tepi jam, setiap kali perubahan negara terjadi.
Mesin Mealy bereaksi lebih cepat terhadap input. Mereka umumnya bereaksi dalam siklus clock yang sama.	Dalam mesin Moore, lebih banyak logika diperlukan untuk memecahkan kode keluaran yang menghasilkan lebih banyak penundaan sirkuit. Mereka umumnya bereaksi satu siklus clock kemudian.

Mesin Moore ke Mesin Mealy

Algoritma 4

Input - Mesin Moore

Output - Mesin Mealy

Langkah 1 - Ambil format tabel transisi Mealy Machine kosong.

Langkah 2 - Salin semua status transisi Mesin Moore ke dalam format tabel ini.

Langkah 3 - Periksa status saat ini dan output yang sesuai di tabel status Mesin Moore; jika untuk status Q i output adalah m, salin ke kolom output dari tabel status Mealy Machine di mana pun Q i muncul di status berikutnya.

Contoh

Mari kita perhatikan mesin Moore berikut -

Keadaan saat ini	Negara bagian selanjutnya		Keluaran
	a = 0	a = 1
→ a	d	b	1
b	Sebuah	d	0
c	c	c	0
d	b	Sebuah	1

Sekarang kita menerapkan Algoritma 4 untuk mengubahnya menjadi Mesin Mealy.

Langkah 1 & 2 -

Keadaan saat ini	Negara bagian selanjutnya
	a = 0		a = 1
	Negara	Keluaran	Negara	Keluaran
→ a	d		b
b	Sebuah		d
c	c		c
d	b		Sebuah

Langkah 3 -

Keadaan saat ini	Negara bagian selanjutnya
	a = 0		a = 1
	Negara	Keluaran	Negara	Keluaran
=> a	d	1	b	0
b	Sebuah	1	d	1
c	c	0	c	0
d	b	0	Sebuah	1

Mesin Mealy ke Mesin Moore

Algoritma 5

Input - Mesin Mealy

Output - Mesin Moore

Langkah 1 - Hitung jumlah output yang berbeda untuk setiap negara (Q i ) yang tersedia di tabel keadaan mesin Mealy.

Langkah 2 - Jika semua output Qi sama, salin status Q i . Jika memiliki n keluaran yang berbeda, pisahkan Q i menjadi n menyatakan sebagai Q di mana n = 0, 1, 2 .......

Langkah 3 - Jika output dari kondisi awal adalah 1, masukkan status awal baru di awal yang memberikan 0 output.

Contoh

Mari kita perhatikan Mesin Mealy berikut -

Keadaan saat ini	Negara bagian selanjutnya
	a = 0		a = 1
	Negara bagian selanjutnya	Keluaran	Negara bagian selanjutnya	Keluaran
→ a	d	0	b	1
b	Sebuah	1	d	0
c	c	1	c	0
d	b	0	Sebuah	1

Di sini, menyatakan 'a' dan 'd' masing-masing hanya memberikan output 1 dan 0, jadi kami mempertahankan status 'a' dan 'd'. Tetapi status 'b' dan 'c' menghasilkan keluaran yang berbeda (1 dan 0). Jadi, kita membagi b menjadi b 0 , b 1 dan c menjadi c 0 , c 1 .

Keadaan saat ini	Negara bagian selanjutnya		Keluaran
	a = 0	a = 1
→ a	d	b 1	1
b 0	Sebuah	d	0
b 1	Sebuah	d	1
c 0	c 1	C 0	0
c 1	c 1	C 0	1
d	b 0	Sebuah	0

Pengantar Tata Bahasa

Dalam pengertian sastra dari istilah tersebut, tata bahasa menunjukkan aturan sintaksis untuk percakapan dalam bahasa alami. Linguistik telah berusaha untuk mendefinisikan tata bahasa sejak awal bahasa alami seperti Inggris, Sanskerta, Mandarin, dll.

Teori bahasa formal menemukan penerapannya secara luas di bidang Ilmu Komputer. Noam Chomsky memberikan model tata bahasa matematika pada tahun 1956 yang efektif untuk menulis bahasa komputer.

Tatabahasa

Tata bahasa G dapat secara formal ditulis sebagai 4-tupel (N, T, S, P) di mana -

• N atau V N adalah seperangkat variabel atau simbol non-terminal.
• T atau ∑ adalah seperangkat simbol Terminal.
• S adalah variabel khusus yang disebut simbol Mulai, S ∈ N
• P adalah aturan produksi untuk Terminal dan Non-terminal. Aturan produksi memiliki bentuk α → β, di mana α dan β adalah string pada V N ∪ β dan setidaknya satu simbol α milik V N.

Contoh

Tata Bahasa G1 -

({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})

Sini,

• S, A, dan B adalah simbol Non-terminal;
• a dan b adalah simbol Terminal
• S adalah simbol Mulai, S ∈ N
• Productions, P: S → AB, A → a, B → b

Contoh

Tata Bahasa G2 -

(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})

Sini,

• S dan A adalah simbol Non-terminal.
• a dan b adalah simbol Terminal.
• ε adalah string kosong.
• S adalah simbol Mulai, S ∈ N
• Produksi P: S → aAb, aA → aaAb, A → ε

Derivasi dari Tata Bahasa

String dapat berasal dari string lain yang menggunakan produksi dalam tata bahasa. Jika tata bahasa G memiliki produksi α → β , kita dapat mengatakan bahwa x α y berasal x β y dalam G. Derivasi ini ditulis sebagai -

x α y ⇒ G x β y

Contoh

Mari kita perhatikan tata bahasanya -

G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})

Beberapa string yang dapat diturunkan adalah -

S ⇒ aA b menggunakan produksi S → aAb

⇒ aA bb menggunakan produksi aA → aAb

⇒ aaa Bbb menggunakan produksi aA → aAb

⇒ aaabbb menggunakan produksi A → ε

Bahasa Dihasilkan oleh Tata Bahasa

Himpunan semua string yang dapat diturunkan dari tata bahasa dikatakan bahasa yang dihasilkan dari tata bahasa itu. Bahasa yang dihasilkan oleh tata bahasa G adalah subset yang didefinisikan secara formal oleh

L (G) = {W | W ∈ ∑ *, S ⇒ G W }

Jika L (G1) = L (G2) , Grammar G1 setara dengan Grammar G2 .

Contoh

Jika ada tata bahasa

G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}

Di sini S menghasilkan AB , dan kita dapat mengganti A dengan a , dan B dengan b . Di sini, satu-satunya string yang diterima adalah ab , yaitu,

L (G) = {ab}

Contoh

Misalkan kita memiliki tata bahasa berikut -

G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA | a, B → bB | b}

Bahasa yang dihasilkan oleh tata bahasa ini -

L (G) = {ab, a 2 b, ab 2 , a 2 b 2 , ………}

= {a m b n | m ≥ 1 dan n ≥ 1}

Konstruksi Tata Bahasa Menghasilkan Bahasa

Kami akan mempertimbangkan beberapa bahasa dan mengubahnya menjadi tata bahasa G yang menghasilkan bahasa tersebut.

Contoh

Masalah - Misalkan, L (G) = {a m b n | m ≥ 0 dan n> 0}. Kita harus mencari tahu tata bahasa G yang menghasilkan L (G) .

Larutan

Karena L (G) = {a m b n | m ≥ 0 dan n> 0}

set string yang diterima dapat ditulis ulang sebagai -

L (G) = {b, ab, bb, aab, abb, …….}

Di sini, simbol awal harus mengambil setidaknya satu 'b' didahului dengan sejumlah 'a' termasuk nol.

Untuk menerima rangkaian string {b, ab, bb, aab, abb, …….}, Kami telah mengambil produksi -

S → aS, S → B, B → b dan B → bB

S → B → b (Diterima)

S → B → bB → bb (Diterima)

S → aS → aB → ab (Diterima)

S → aS → aaS → aaB → aab (Diterima)

S → aS → aB → abB → abb (Diterima)

Dengan demikian, kita dapat membuktikan bahwa setiap string tunggal dalam L (G) diterima oleh bahasa yang dihasilkan oleh set produksi.

Oleh karena itu tata bahasa -

G: ({S, A, B}, {a, b}, S, {S → aS | B, B → b | bB})

Contoh

Masalah - Misalkan, L (G) = {a m b n | m> 0 dan n ≥ 0}. Kita harus mencari tahu tata bahasa G yang menghasilkan L (G).

Solusi -

Karena L (G) = {a m b n | m> 0 dan n ≥ 0}, set string yang diterima dapat ditulis ulang sebagai -

L (G) = {a, aa, ab, aaa, aab, abb, …….}

Di sini, simbol awal harus mengambil setidaknya satu 'a' diikuti oleh sejumlah 'b' termasuk nol.

Untuk menerima rangkaian string {a, aa, ab, aaa, aab, abb, …….}, Kami telah mengambil produksi -

S → aA, A → aA, A → B, B → bB, B → λ

S → aA → aB → aλ → a (Diterima)

S → aA → aaA → aaB → aaλ → aa (Diterima)

S → aA → aB → abB → abλ → ab (Diterima)

S → aA → aaA → aaaA → aaaB → aaaλ → aaa (Diterima)

S → aA → aa → aaB → aabB → aabλ → aab (Diterima)

S → aA → aB → abB → abb → abbλ → abb (Diterima)

Dengan demikian, kita dapat membuktikan bahwa setiap string tunggal dalam L (G) diterima oleh bahasa yang dihasilkan oleh set produksi.

Oleh karena itu tata bahasa -

G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB})

Klasifikasi Tata Bahasa Chomsky

Menurut Noam Chomosky, ada empat jenis tata bahasa - Tipe 0, Tipe 1, Tipe 2, dan Tipe 3. Tabel berikut menunjukkan bagaimana mereka berbeda satu sama lain -

Tipe Tata Bahasa	Tata Bahasa Diterima	Bahasa diterima	Otomat
Ketik 0	Tata bahasa yang tidak dibatasi	Bahasa enumerable rekursif	Mesin Turing
Tipe 1	Tata bahasa yang sensitif terhadap konteks	Bahasa yang sensitif terhadap konteks	Otomat yang dibatasi linier
Tipe 2	Tata bahasa bebas konteks	Bahasa bebas konteks	Automat pushdown
Tipe 3	Tata bahasa biasa	Bahasa biasa	Otomat keadaan terbatas

Lihatlah ilustrasi berikut. Ini menunjukkan ruang lingkup masing-masing jenis tata bahasa -

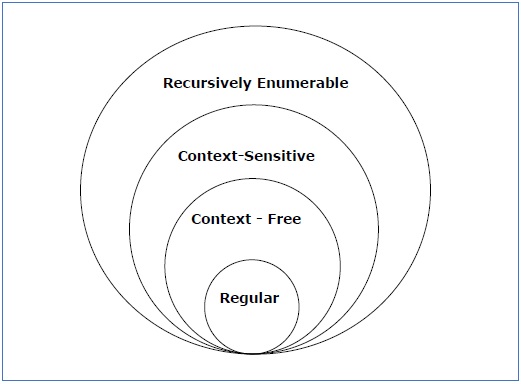
Tipe - 3 Tata Bahasa

Tata bahasa tipe-3 menghasilkan bahasa biasa. Tata bahasa tipe-3 harus memiliki non-terminal tunggal di sisi kiri dan sisi kanan yang terdiri dari terminal tunggal atau terminal tunggal diikuti oleh non-terminal tunggal.

Produksi harus dalam bentuk X → a atau X → aY

di mana X, Y ∈ N (Non terminal)

dan ∈ T (Terminal)

Aturan S → ε diizinkan jika S tidak muncul di sebelah kanan aturan apa pun.

Contoh

X → ε 
X → a | aY
Y → b 

Tipe - 2 Tata Bahasa

Tata bahasa tipe-2 menghasilkan bahasa bebas konteks.

Produksi harus dalam bentuk A → γ

di mana A ∈ N (Non terminal)

dan γ ∈ (T ∪ N) * (String terminal dan non-terminal).

Bahasa-bahasa ini yang dihasilkan oleh tata bahasa ini dikenali oleh otomat pushdown non-deterministik.

Contoh

S → X a 
X → a 
X → aX 
X → abc 
X → ε

Tipe - 1 Tata Bahasa

Tata bahasa tipe-1 menghasilkan bahasa konteks-sensitif. Produksi harus dalam bentuk

α A β → α γ β

di mana A ∈ N (Non-terminal)

dan α, β, γ ∈ (T ∪ N) * (String terminal dan non-terminal)

String α dan β mungkin kosong, tetapi γ harus tidak kosong.

Aturan S → ε diizinkan jika S tidak muncul di sebelah kanan aturan apa pun. Bahasa yang dihasilkan oleh tata bahasa ini dikenali oleh otomat terikat linier.

Contoh

AB → AbBc 
A → bcA 
B → b 

Tipe - 0 Tata Bahasa

Tata bahasa tipe-0 menghasilkan bahasa yang dapat dihitung berulang secara rekursif. Produksi tidak memiliki batasan. Mereka adalah setiap tata bahasa struktur fase termasuk semua tata bahasa formal.

Mereka menghasilkan bahasa yang dikenali oleh mesin Turing.

Produksi dapat dalam bentuk α → β di mana α adalah string terminal dan nonterminals dengan setidaknya satu non-terminal dan α tidak boleh nol. β adalah rangkaian terminal dan non-terminal.

Contoh

S → ACaB 
Bc → acB 
CB → DB 
aD → Db 

Ekspresi Reguler

Ekspresi Reguler dapat didefinisikan secara rekursif sebagai berikut -

• ε adalah Ekspresi Reguler yang menunjukkan bahasa yang berisi string kosong. (L (ε) = {ε})
• φ adalah Ekspresi Reguler yang menunjukkan bahasa kosong. (L (φ) = {})
• x adalah Ekspresi Reguler di mana L = {x}
• Jika X adalah Ekspresi Reguler yang menunjukkan bahasa L (X) dan Y adalah Ekspresi Reguler yang menunjukkan bahasa L (Y) , maka
  • X + Y adalah Ekspresi Reguler yang sesuai dengan bahasa L (X) ∪ L (Y) di mana L (X + Y) = L (X) ∪ L (Y) .
  • X. Y adalah Ekspresi Reguler yang sesuai dengan bahasa L (X). L (Y) di mana L (XY) = L (X). L (Y)
  • R * adalah Ekspresi Reguler yang sesuai dengan bahasa L (R *) di mana L (R *) = (L (R)) *
• Jika kami menerapkan salah satu aturan beberapa kali dari 1 hingga 5, itu adalah Ekspresi Reguler.

Beberapa Contoh RE

Ekspresi Reguler	Set Reguler
(0 + 10 *)	L = {0, 1, 10, 100, 1000, 10000,…}
(0 * 10 *)	L = {1, 01, 10, 010, 0010, ...}
(0 + ε) (1 + ε)	L = {ε, 0, 1, 01}
(a + b) *	Set string a dan b dari panjang apa pun termasuk string nol. Jadi L = {ε, a, b, aa, ab, bb, ba, aaa …….}
(a + b) * abb	Set string a dan b yang diakhiri dengan string abb. Jadi L = {abb, aabb, babb, aaabb, ababb, ………… ..}
(11) *	Set yang terdiri dari bilangan genap 1 termasuk string kosong, So L = {ε, 11, 1111, 111111, ……….}
(aa) * (bb) * b	Set string yang terdiri dari bilangan genap a diikuti dengan bilangan ganjil dari b, jadi L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, ………… ..}
(aa + ab + ba + bb) *	String a dan b dengan panjang genap dapat diperoleh dengan menggabungkan setiap kombinasi dari string aa, ab, ba dan bb termasuk null, jadi L = {aa, ab, ba, bb, aaab, aaba, ………… .. }

Set Reguler

Set apa pun yang mewakili nilai Ekspresi Reguler disebut Set Reguler.

Properti Set Reguler

Properti 1 . Penyatuan dua set reguler adalah teratur.

Bukti -

Mari kita ambil dua ekspresi reguler

RE 1 = a (aa) * dan RE 2 = (aa) *

Jadi, L 1 = {a, aaa, aaaaa, .....} (String dengan panjang aneh tidak termasuk Null)

dan L 2 = {ε, aa, aaaa, aaaaaa, .......} (String dengan panjang genap termasuk Null)

L 1 ∪ L 2 = {ε, a, aa, aaa, aaaa, aaaaa, aaaaaa, .......}

(String dari semua panjang yang mungkin termasuk Null)

RE (L 1 ∪ L 2 ) = a * (yang merupakan ekspresi reguler itu sendiri)

Karena itu terbukti.

Properti 2. Perpotongan dua set reguler adalah teratur.

Bukti -

Mari kita ambil dua ekspresi reguler

RE 1 = a (a *) dan RE 2 = (aa) *

Jadi, L 1 = {a, aa, aaa, aaaa, ....} (String dari semua panjang yang mungkin tidak termasuk Null)

L 2 = {ε, aa, aaaa, aaaaaa, .......} (String dengan panjang genap termasuk Null)

L 1 ∩ L 2 = {aa, aaaa, aaaaaa, .......} (String dengan panjang genap tidak termasuk Null)

RE (L 1 ∩ L 2 ) = aa (aa) * yang merupakan ekspresi reguler itu sendiri.

Karena itu terbukti.

Properti 3. Komplemen dari set reguler adalah teratur.

Bukti -

Mari kita ambil ekspresi reguler -

RE = (aa) *

Jadi, L = {ε, aa, aaaa, aaaaaa, .......} (String dengan panjang genap termasuk Null)

Komplemen L adalah semua string yang tidak ada dalam L.

Jadi, L '= {a, aaa, aaaaa, .....} (String dengan panjang aneh tidak termasuk Null)

RE (L ') = a (aa) * yang merupakan ekspresi reguler itu sendiri.

Karena itu terbukti.

Properti 4. Perbedaan dari dua set reguler adalah reguler.

Bukti -

Mari kita ambil dua ekspresi reguler -

RE 1 = a (a *) dan RE 2 = (aa) *

Jadi, L 1 = {a, aa, aaa, aaaa, ....} (String dari semua panjang yang mungkin tidak termasuk Null)

L 2 = {ε, aa, aaaa, aaaaaa, .......} (String dengan panjang genap termasuk Null)

L 1 - L 2 = {a, aaa, aaaaa, aaaaaaa, ....}

(String dari semua panjang aneh tidak termasuk Null)

RE (L 1 - L 2 ) = a (aa) * yang merupakan ekspresi reguler.

Karena itu terbukti.

Properti 5. Pembalikan set reguler adalah teratur.

Bukti -

Kita harus membuktikan LR juga teratur jika L adalah himpunan biasa.

Biarkan, L = {01, 10, 11, 10}

RE (L) = 01 + 10 + 11 + 10

L R = {10, 01, 11, 01}

RE (L R ) = 01 + 10 + 11 + 10 yang teratur

Karena itu terbukti.

Properti 6. Penutupan set reguler adalah teratur.

Bukti -

Jika L = {a, aaa, aaaaa, .......} (String dengan panjang aneh tidak termasuk Null)

yaitu, RE (L) = a (aa) *

L * = {a, aa, aaa, aaaa, aaaaa, ……………} (String dari semua panjang tidak termasuk Null)

RE (L *) = a (a) *

Karena itu terbukti.

Properti 7. Rangkuman dua set reguler teratur.

Bukti -

Biarkan RE 1 = (0 + 1) * 0 dan RE 2 = 01 (0 + 1) *

Di sini, L 1 = {0, 00, 10, 000, 010, ......} (Set string berakhir dengan 0)

dan L 2 = {01, 010.011, .....} (Set string yang dimulai dengan 01)

Kemudian, L 1 L 2 = {001,0010,0011,0001,00010,00011,1001,10010, .............}

Set string yang mengandung 001 sebagai substring yang dapat diwakili oleh RE - (0 + 1) * 001 (0 + 1) *

Karena itu terbukti.

Identitas Terkait dengan Ekspresi Reguler

Diberikan R, P, L, Q sebagai ekspresi reguler, identitas berikut berlaku -

• ∅ * = ε
• ε * = ε
• RR * = R * R
• R * R * = R *
• (R *) * = R *
• RR * = R * R
• (PQ) * P = P (QP) *
• (a + b) * = (a * b *) * = (a * + b *) * = (a + b *) * = a * (ba *) *
• R + ∅ = ∅ + R = R (Identitas untuk penyatuan)
• R ε = ε R = R (Identitas untuk penyatuan)
• ∅ L = L ∅ = ∅ (annihilator untuk penggabungan)
• R + R = R (Hukum idempoten)
• L (M + N) = LM + LN (Hukum distributif kiri)
• (M + N) L = ML + NL (Hukum distributif kanan)
• ε + RR * = ε + R * R = R *

Teorema Arden

Untuk mengetahui ekspresi reguler dari Automaton Terbatas, kami menggunakan Teorema Arden bersama dengan properti ekspresi reguler.

Pernyataan -

Biarkan P dan Q menjadi dua ekspresi reguler.

Jika P tidak mengandung string nol, maka R = Q + RP memiliki solusi unik yaitu R = QP *

Bukti -

R = Q + (Q + RP) P [Setelah memberi nilai R = Q + RP]

= Q + QP + RPP

Ketika kami menempatkan nilai R berulang secara berulang, kami mendapatkan persamaan berikut -

R = Q + QP + QP 2 + QP 3 … ..

R = Q (ε + P + P 2 + P 3 +….)

R = QP * [Sebagai P * mewakili (ε + P + P2 + P3 +….)]

Karena itu terbukti.

Asumsi untuk Menerapkan Teorema Arden

• Diagram transisi tidak boleh memiliki transisi NULL
• Itu harus hanya memiliki satu keadaan awal

metode

Langkah 1 - Buat persamaan sebagai bentuk berikut untuk semua status DFA yang memiliki n status dengan status awal q 1 .

q 1 = q 1 R 11 + q 2 R 21 +… + q n R n1 + ε

q 2 = q 1 R 12 + q 2 R 22 +… + q n R n2

…………………………

…………………………

…………………………

…………………………

q n = q 1 R 1n + q 2 R 2n +… + q n R nn

R ij mewakili himpunan label tepi dari q i ke q j , jika tidak ada tepi seperti itu, maka R ij = ∅

Langkah 2 - Selesaikan persamaan ini untuk mendapatkan persamaan untuk kondisi akhir dalam hal R ij

Masalah

Bangun ekspresi reguler yang sesuai dengan automata yang diberikan di bawah ini -

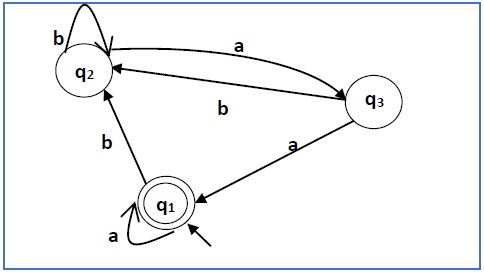
Solusi -

Di sini kondisi awal dan akhir adalah q 1 .

Persamaan untuk tiga negara q1, q2, dan q3 adalah sebagai berikut -

q 1 = q 1 a + q 3 a + ε (ε bergerak karena q1 adalah keadaan awal0

q 2 = q 1 b + q 2 b + q 3 b

q 3 = q 2 a

Sekarang, kita akan menyelesaikan tiga persamaan ini -

q 2 = q 1 b + q 2 b + q 3 b

= q 1 b + q 2 b + (q 2 a) b (Mengganti nilai q 3 )

= q 1 b + q 2 (b + ab)

= q 1 b (b + ab) * (Menerapkan Teorema Arden)

q 1 = q 1 a + q 3 a + ε

= q 1 a + q 2 aa + ε (Mengganti nilai q 3 )

= q 1 a + q 1 b (b + ab *) aa + ε (Mengganti nilai q 2 )

= q 1 (a + b (b + ab) * aa) + ε

= ε (a + b (b + ab) * aa) *

= (a + b (b + ab) * aa) *

Oleh karena itu, ekspresi regulernya adalah (a + b (b + ab) * aa) *.

Masalah

Bangun ekspresi reguler yang sesuai dengan automata yang diberikan di bawah ini -

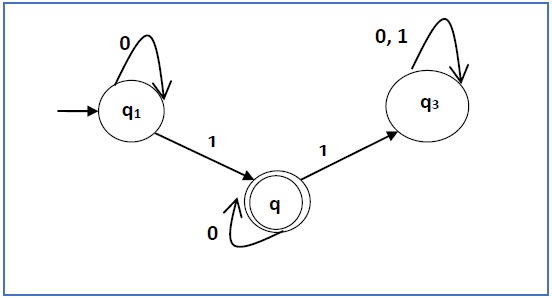
Solusi -

Di sini kondisi awal adalah q 1 dan kondisi akhir adalah q 2

Sekarang kita menuliskan persamaan -

q 1 = q 1 0 + ε

q 2 = q 1 1 + q 2 0

q 3 = q 2 1 + q 3 0 + q 3 1

Sekarang, kita akan menyelesaikan tiga persamaan ini -

q 1 = ε0 * [As, εR = R]

Jadi, q 1 = 0 *

q 2 = 0 * 1 + q 2 0

Jadi, q 2 = 0 * 1 (0) * [Oleh teorema Arden]

Oleh karena itu, ekspresi regulernya adalah 0 * 10 *.

Pembangunan FA dari RE

Kita dapat menggunakan Konstruksi Thompson untuk mencari tahu Otomat Terbatas dari Ekspresi Reguler. Kami akan mengurangi ekspresi reguler menjadi ekspresi reguler terkecil dan mengubahnya menjadi NFA dan akhirnya menjadi DFA.

Beberapa ekspresi RA dasar adalah sebagai berikut -

Kasus 1 - Untuk ekspresi reguler 'a', kita dapat membuat FA berikut -

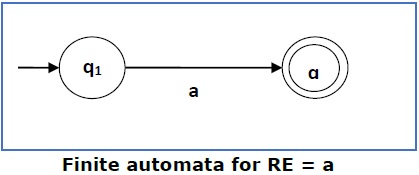
Kasus 2 - Untuk ekspresi reguler 'ab', kita dapat membuat FA berikut -

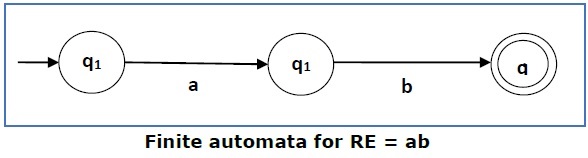
Kasus 3 - Untuk ekspresi reguler (a + b), kita dapat membuat FA berikut -

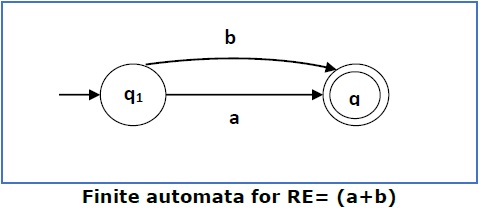
Kasus 4 - Untuk ekspresi reguler (a + b) *, kita dapat membuat FA berikut -

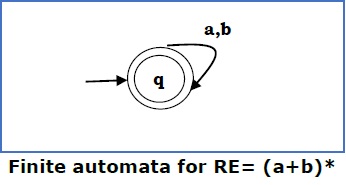
metode

Langkah 1 Buat NFA dengan Null bergerak dari ekspresi reguler yang diberikan.

Langkah 2 Hapus Null transisi dari NFA dan mengubahnya menjadi DFA yang setara.

Masalah

Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0

Solution

We will concatenate three expressions "1", "(0 + 1)*" and "0"

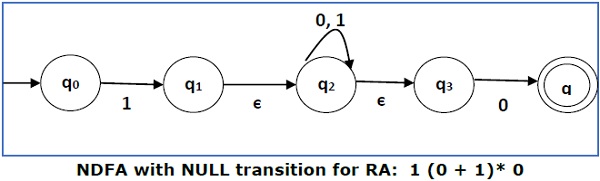
Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

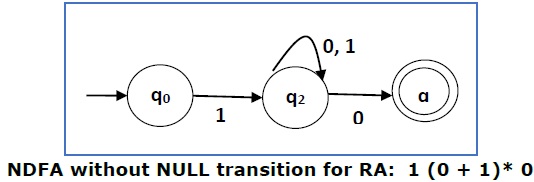
It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.

Finite Automata with Null Moves (NFA-ε)

A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move .

An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q 0 , F), consisting of

• Q − a finite set of states
• ∑ − a finite set of input symbols
• δ − a transition function δ : Q × (∑ ∪ {ε}) → 2 Q
• q 0 − an initial state q 0 ∈ Q
• F − a set of final state/states of Q (F⊆Q).

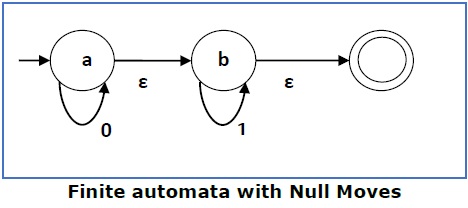
The above (FA-ε) accepts a string set − {0, 1, 01}

Removal of Null Moves from Finite Automata

If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −

• Find all the outgoing edges from Y.
• Copy all these edges starting from X without changing the edge labels.
• If X is an initial state, make Y also an initial state.
• If Y is a final state, make X also a final state.

Masalah

Convert the following NFA-ε to NFA without Null move.

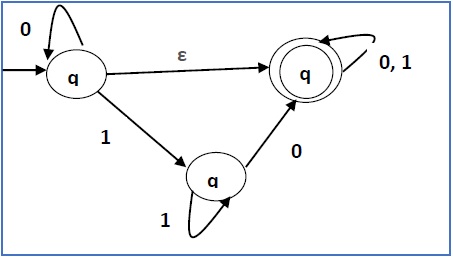
Solution

Step 1 −

Here the ε transition is between q 1 and q 2 , so let q 1 is X and q f is Y .

Here the outgoing edges from q f is to q f for inputs 0 and 1.

Step 2 −

Now we will Copy all these edges from q 1 without changing the edges from q f and get the following FA −

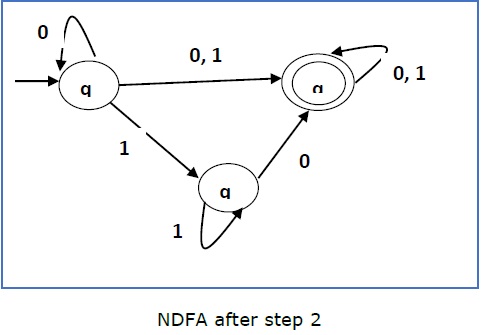
Step 3 −

Here q 1 is an initial state, so we make q f also an initial state.

So the FA becomes −

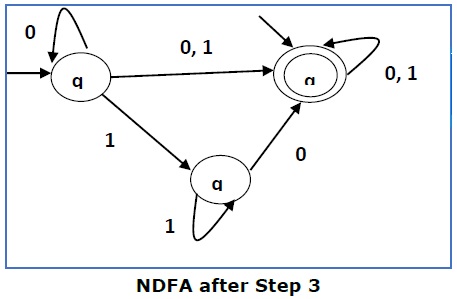
Step 4 −

Here q f is a final state, so we make q 1 also a final state.

So the FA becomes −

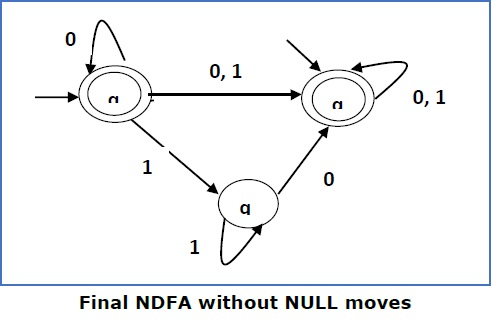
Pumping Lemma For Regular Grammars

Dalil

Let L be a regular language. Then there exists a constant 'c' such that for every string w in L −

| w | ≥ c

We can break w into three strings, w = xyz , such that −

• |y| > 0
• |xy| ≤ c
• For all k ≥ 0, the string xy k z is also in L.

Applications of Pumping Lemma

Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.

• If L is regular, it satisfies Pumping Lemma.
• If L does not satisfy Pumping Lemma, it is non-regular.

Method to prove that a language L is not regular

• At first, we have to assume that L is regular.
• So, the pumping lemma should hold for L .
• Use the pumping lemma to obtain a contradiction −
  • Select w such that |w| ≥ c
  • Select y such that |y| ≥ 1
  • Select x such that |xy| ≤ c
  • Assign the remaining string to z.
  • Select k such that the resulting string is not in L.

Hence L is not regular.

Masalah

Prove that L = {a i b i | i ≥ 0} is not regular.

Solution −

• At first, we assume that L is regular and n is the number of states.
• Let w = a n b n . Thus |w| = 2n ≥ n.
• By pumping lemma, let w = xyz, where |xy| ≤ n.
• Let x = a p , y = a q , and z = a r b n , where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
• Misalkan k = 2. Kemudian xy 2 z = a p a 2q a r b n .
• Jumlah as = (p + 2q + r) = (p + q + r) + q = n + q
• Karenanya, xy 2 z = a n + q b n . Karena q ≠ 0, xy 2 z bukan dari bentuk a n b n .
• Jadi, xy 2 z tidak dalam L. Oleh karena itu L tidak teratur.

Komplemen DFA

Jika (Q, ∑, δ, q 0 , F) menjadi DFA yang menerima bahasa L, maka komplemen DFA dapat diperoleh dengan menukar negara penerima dengan negara yang tidak menerima dan sebaliknya.

Kami akan mengambil contoh dan menguraikannya di bawah ini -

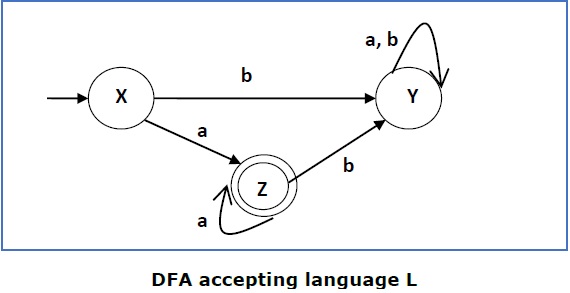
DFA ini menerima bahasa

L = {a, aa, aaa, .............}

di atas alfabet

Β = {a, b}

Jadi, RE = a + .

Sekarang kita akan menukar negara penerima dengan negara tidak menerima dan sebaliknya dan akan mendapatkan yang berikut -

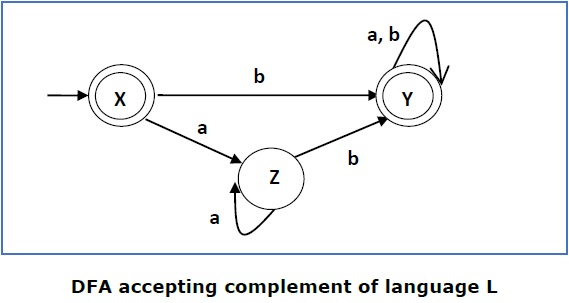
DFA ini menerima bahasa

Ľ = {ε, b, ab, bb, ba, ...............}

di atas alfabet

Β = {a, b}

Catatan - Jika kita ingin melengkapi NFA, kita harus terlebih dahulu mengubahnya menjadi DFA dan kemudian harus menukar status seperti pada metode sebelumnya.

Pengantar Tata Bahasa Bebas Konteks

Definisi - Tata bahasa bebas konteks (CFG) yang terdiri dari seperangkat aturan tata bahasa yang terbatas adalah empat kali lipat (N, T, P, S) di mana

• N adalah seperangkat simbol non-terminal.
• T adalah seperangkat terminal di mana N ∩ T = NULL.
• P adalah seperangkat aturan, P: N → (N ∪ T) * , yaitu sisi kiri dari aturan produksi P memang memiliki konteks kanan atau konteks kiri.
• S adalah simbol awal.

Contoh

• Tata bahasa ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
• Tata bahasanya ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
• Tata bahasanya ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε

Generasi Derivation Tree

Pohon derivasi atau pohon parse adalah pohon berakar tertata yang secara grafis mewakili informasi semantik string yang berasal dari tata bahasa bebas konteks.

Teknik Representasi

• Root vertex - Harus diberi label oleh simbol awal.
• Vertex - Dilabeli oleh simbol non-terminal.
• Daun - Ditandai dengan simbol terminal atau ε.

Jika S → x 1 x 2 …… x n adalah aturan produksi dalam CFG, maka pohon parse / pohon derivasi adalah sebagai berikut -

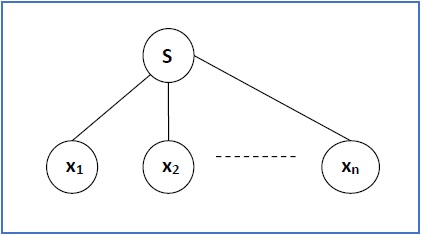
Ada dua pendekatan berbeda untuk menggambar pohon derivasi -

Pendekatan Top-down -

• Mulai dengan simbol awal S
• Turun ke daun pohon menggunakan produksi

Pendekatan Bottom-up -

• Mulai dari daun pohon
• Lanjutkan ke atas ke root yang merupakan simbol awal S

Derivasi atau Yield of a Tree

Derivasi atau hasil pohon parse adalah string terakhir yang diperoleh dengan menggabungkan label daun pohon dari kiri ke kanan, mengabaikan Nulls. Namun, jika semua daunnya Null, turunannya adalah Null.

Contoh

Biarkan CFG {N, T, P, S} menjadi

N = {S}, T = {a, b}, simbol awal = S, P = S → SS | aSb | ε

Salah satu derivasi dari CFG di atas adalah "abaabb"

S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

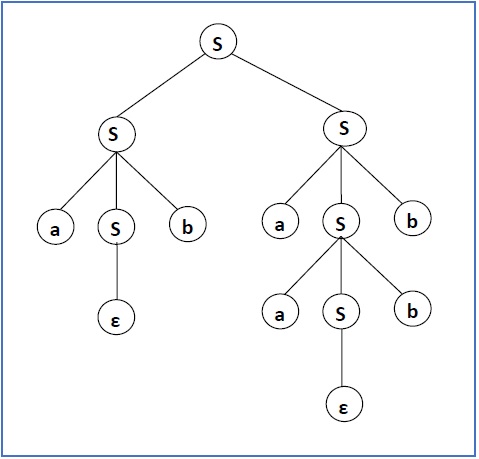
Bentuk Sentensial dan Pohon Derivasi Parsial

Pohon turunan parsial adalah sub-pohon dari pohon derivasi / pohon parse sehingga semua anak-anaknya berada di dalam sub-pohon atau tidak ada dari mereka yang berada di dalam sub-pohon.

Contoh

Jika dalam CFG apa pun produksinya adalah -

S → AB, A → aaA | ε, B → Bb | ε

pohon derivasi parsial dapat menjadi sebagai berikut -

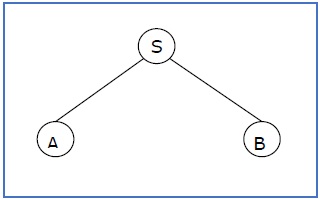
Jika pohon derivasi parsial mengandung akar S, itu disebut bentuk sentensial . Sub-pohon di atas juga dalam bentuk sentensial.

Derivasi String yang Paling Kiri dan Paling Kanan

• Derivasi paling kiri - Derivasi paling kiri diperoleh dengan menerapkan produksi ke variabel paling kiri di setiap langkah.
• Derivasi paling kanan - Derivasi paling kanan diperoleh dengan menerapkan produksi ke variabel paling kanan di setiap langkah.

Contoh

Biarkan seperangkat aturan produksi dalam CFG menjadi

X → X + X | X * X | X | Sebuah

lebih dari satu alfabet {a}.

Derivasi paling kiri untuk string "a + a * a" mungkin -

X → X + X → a + X → a + X * X → a + a * X → a + a * a

Derivasi bertahap dari string di atas ditunjukkan seperti di bawah ini -

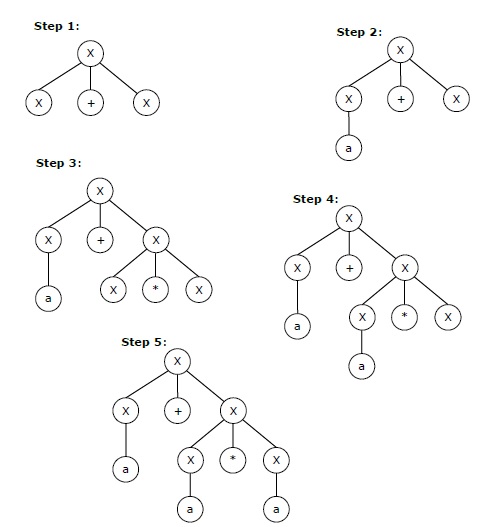
Derivasi paling kanan untuk string di atas "a + a * a" mungkin -

X → X * X → X * a → X + X * a → X + a * a → a + a * a

Derivasi bertahap dari string di atas ditunjukkan seperti di bawah ini -

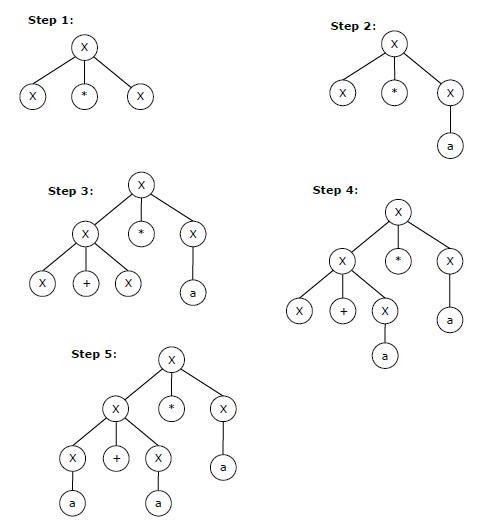
Tata Bahasa Rekursif Kiri dan Kanan

Dalam tata bahasa G bebas konteks, jika ada produksi dalam bentuk X → Xa di mana X adalah non-terminal dan 'a' adalah serangkaian terminal, itu disebut produksi rekursif kiri . Tata bahasa yang memiliki produksi rekursif kiri disebut tata bahasa rekursif kiri .

Dan jika dalam tata bahasa G bebas konteks, jika ada produksi dalam bentuk X → aX di mana X adalah non-terminal dan 'a' adalah serangkaian terminal, itu disebut produksi rekursif yang tepat . Tata bahasa yang memiliki produksi rekursif yang tepat disebut tata bahasa recursive yang tepat .

Ambiguitas dalam Tata Bahasa Bebas Konteks

Jika konteks bebas tata bahasa G memiliki lebih dari satu pohon derivasi untuk beberapa string w ∈ L (G) , itu disebut tata bahasa ambigu . Ada beberapa derivasi paling kanan atau paling kiri untuk beberapa string yang dihasilkan dari tata bahasa itu.

Masalah

Periksa apakah tata bahasa G dengan aturan produksi -

X → X + X | X * X | X | Sebuah

ambigu atau tidak.

Larutan

Let's find out the derivation tree for the string "a+a*a". It has two leftmost derivations.

Derivation 1 − X → X+X → a +X → a+ X*X → a+a*X → a+a*a

Parse tree 1 −

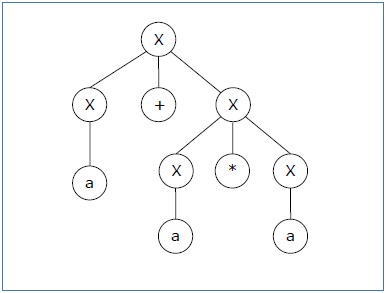
Derivation 2 − X → X*X → X+X*X → a+ X*X → a+a*X → a+a*a

Parse tree 2 −

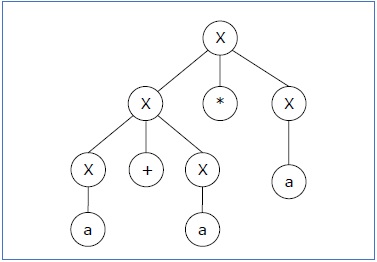
Since there are two parse trees for a single string "a+a*a", the grammar G is ambiguous.

CFL Closure Property

Context-free languages are closed under −

• Persatuan
• Rangkaian
• Kleene Star operation

Persatuan

Let L 1 and L 2 be two context free languages. Then L 1 ∪ L 2 is also context free.

Contoh

Let L 1 = { a n b n , n > 0}. Corresponding grammar G 1 will have P: S1 → aAb|ab

Let L 2 = { c m d m , m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| ε

Union of L 1 and L 2 , L = L 1 ∪ L 2 = { a n b n } ∪ { c m d m }

The corresponding grammar G will have the additional production S → S1 | S2

Rangkaian

If L 1 and L 2 are context free languages, then L 1 L 2 is also context free.

Contoh

Union of the languages L 1 and L 2 , L = L 1 L 2 = { a n b n c m d m }

The corresponding grammar G will have the additional production S → S1 S2

Kleene Star

If L is a context free language, then L* is also context free.

Contoh

Let L = { a n b n , n ≥ 0}. Corresponding grammar G will have P: S → aAb| ε

Kleene Star L 1 = { a n b n }*

The corresponding grammar G 1 will have additional productions S1 → SS 1 | ε

Context-free languages are not closed under −

• Intersection − If L1 and L2 are context free languages, then L1 ∩ L2 is not necessarily context free.
• Intersection with Regular Language − If L1 is a regular language and L2 is a context free language, then L1 ∩ L2 is a context free language.
• Complement − If L1 is a context free language, then L1' may not be context free.

CFG Simplification

In a CFG, it may happen that all the production rules and symbols are not needed for the derivation of strings. Besides, there may be some null productions and unit productions. Elimination of these productions and symbols is called simplification of CFGs . Simplification essentially comprises of the following steps −

• Reduction of CFG
• Removal of Unit Productions
• Removal of Null Productions

Reduction of CFG

CFGs are reduced in two phases −

Phase 1 − Derivation of an equivalent grammar, G' , from the CFG, G , such that each variable derives some terminal string.

Derivation Procedure −

Step 1 − Include all symbols, W 1 , that derive some terminal and initialize i=1 .

Langkah 2 - Sertakan semua simbol, W i + 1 , yang berasal W i .

Langkah 3 - Bertambah i dan ulangi Langkah 2, hingga W i + 1 = W i .

Langkah 4 - Sertakan semua aturan produksi yang memiliki W i di dalamnya.

Fase 2 - Turunnya tata bahasa setara, G ” , dari CFG, G ' , sehingga setiap simbol muncul dalam bentuk sentensial.

Prosedur Derivasi -

Langkah 1 - Sertakan simbol mulai di Y 1 dan inisialisasi i = 1 .

Langkah 2 - Sertakan semua simbol, Y i + 1 , yang dapat diturunkan dari Y i dan sertakan semua aturan produksi yang telah diterapkan.

Langkah 3 - Bertambah i dan ulangi Langkah 2, sampai Y i + 1 = Y i .

Masalah

Temukan tata bahasa berkurang setara dengan tata bahasa G, memiliki aturan produksi, P: S → AC | B, A → a, C → c | BC, E → aA | e

Larutan

Fase 1 -

T = {a, c, e}

W 1 = {A, C, E} dari aturan A → a, C → c dan E → aA

W 2 = {A, C, E} U {S} dari aturan S → AC

W 3 = {A, C, E, S} U ∅

Karena W 2 = W 3 , kita dapat menurunkan G 'sebagai -

G '= {{A, C, E, S}, {a, c, e}, P, {S}}

di mana P: S → AC, A → a, C → c, E → aA | e

Fase 2 -

Y 1 = {S}

Y 2 = {S, A, C} dari aturan S → AC

Y 3 = {S, A, C, a, c} dari aturan A → a dan C → c

Y 4 = {S, A, C, a, c}

Karena Y 3 = Y 4 , kita dapat memperoleh G ”sebagai -

G ”= {{A, C, S}, {a, c}, P, {S}}

di mana P: S → AC, A → a, C → c

Penghapusan Produksi Unit

Setiap aturan produksi dalam bentuk A → B di mana A, B ∈ Non-terminal disebut unit produksi. .

Prosedur Penghapusan -

Step 1 − To remove A → B , add production A → x to the grammar rule whenever B → x occurs in the grammar. [x ∈ Terminal, x can be Null]

Step 2 − Delete A → B from the grammar.

Step 3 − Repeat from step 1 until all unit productions are removed.

Masalah

Remove unit production from the following −

S → XY, X → a, Y → Z | b, Z → M, M → N, N → a

Solution −

There are 3 unit productions in the grammar −

Y → Z, Z → M, and M → N

At first, we will remove M → N.

As N → a, we add M → a, and M → N is removed.

The production set becomes

S → XY, X → a, Y → Z | b, Z → M, M → a, N → a

Now we will remove Z → M.

As M → a, we add Z→ a, and Z → M is removed.

The production set becomes

S → XY, X → a, Y → Z | b, Z → a, M → a, N → a

Now we will remove Y → Z.

As Z → a, we add Y→ a, and Y → Z is removed.

The production set becomes

S → XY, X → a, Y → a | b, Z → a, M → a, N → a

Now Z, M, and N are unreachable, hence we can remove those.

The final CFG is unit production free −

S → XY, X → a, Y → a | b

Removal of Null Productions

In a CFG, a non-terminal symbol 'A' is a nullable variable if there is a production A → ε or there is a derivation that starts at A and finally ends up with

ε: A → .......… → ε

Removal Procedure

Step 1 − Find out nullable non-terminal variables which derive ε.

Langkah 2 - Untuk setiap produksi A → a , buat semua produksi A → x di mana x diperoleh dari 'a' dengan menghapus satu atau beberapa non-terminal dari Langkah 1.

Langkah 3 - Gabungkan produksi asli dengan hasil langkah 2 dan hapus ε - produksi .

Masalah

Hapus produksi nol dari yang berikut -

S → ASA | aB | b, A → B, B → b | ∈

Solusi -

Ada dua variabel yang dapat dibatalkan - A dan B

Pada awalnya, kami akan menghapus B → ε.

Setelah menghapus B → ε , set produksi menjadi -

S → ASA | aB | b | a, A ε B | b | & epsilon, B → b

Sekarang kita akan menghapus A → ε.

Setelah menghapus A → ε , set produksi menjadi -

S → ASA | aB | b | a |SA | SEBAGAI | S, A → B | b, B → b

Ini adalah set produksi akhir tanpa transisi nol.

Bentuk Normal Chomsky

CFG dalam Bentuk Normal Chomsky jika Productions dalam bentuk berikut -

• A → a
• A → SM
• S → ε

di mana A, B, dan C adalah non-terminal dan a adalah terminal.

Algoritma untuk Mengkonversi ke Bentuk Normal Chomsky -

Langkah 1 - Jika simbol awal S terjadi pada beberapa sisi kanan, membuat simbol awal baru S ' dan produksi baru S' → S .

Langkah 2 - Hapus produksi Null. (Menggunakan algoritma penghapusan produksi Null dibahas sebelumnya)

Langkah 3 - Hapus produksi unit. (Menggunakan algoritma penghapusan produksi Unit yang dibahas sebelumnya)

Langkah 4 - Ganti setiap produksi A → B 1 ... B n di mana n> 2 dengan A → B 1 C di mana C → B 2 ... B n . Ulangi langkah ini untuk semua produksi yang memiliki dua atau lebih simbol di sisi kanan.

Langkah 5 - Jika sisi kanan dari setiap produksi adalah dalam bentuk A → aB di mana a adalah terminal dan A, B adalah non-terminal, maka produksi digantikan oleh A → XB dan X → a . Ulangi langkah ini untuk setiap produksi yang dalam bentuk A → aB .

Masalah

Ubah CFG berikut menjadi CNF

S → ASA | aB, A → B | S, B → b | ε

Larutan

(1) Karena S muncul di RHS, kami menambahkan status baru S 0 dan S 0 → S ditambahkan ke set produksi dan menjadi -

S 0 → S, S → ASA | aB, A → B | S, B → b | ∈

(2) Sekarang kami akan menghapus produksi nol -

B → ∈ dan A → ∈

After removing B → ε, the production set becomes −

S 0 →S, S→ ASA | aB | a, A → B | S | ∈, B → b

After removing A → ∈, the production set becomes −

S 0 →S, S→ ASA | aB | a | AS | SA | S, A → B | S, B → b

(3) Now we will remove the unit productions.

After removing S → S, the production set becomes −

S 0 →S, S→ ASA | aB | a | AS | SA, A → B | S, B → b

After removing S 0 → S, the production set becomes −

S 0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA

A → B | S, B → b

After removing A→ B, the production set becomes −

S 0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA

A → S | b

B → b

After removing A→ S, the production set becomes −

S 0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA

A → b |ASA | aB | a | AS | SA, B → b

(4) Now we will find out more than two variables in the RHS

Here, S 0 → ASA, S → ASA, A→ ASA violates two Non-terminals in RHS

Hence we will apply step 4 and step 5 to get the following final production set which is in CNF −

S 0 → AX | aB | a | AS | SA

S→ AX | aB | a | AS | SA

A → b |AX | aB | a | AS | SA

B → b

X → SA

(5) We have to change the productions S 0 → aB, S→ aB, A→ aB

And the final production set becomes −

S 0 → AX | YB | a | AS | SA

S→ AX | YB | a | AS | SA

A → b A → b |AX | YB | a | AS | SA

B → b

X → SA

Y → a

Greibach Normal Form

A CFG is in Greibach Normal Form if the Productions are in the following forms −

A → b

A → bD 1 …D n

S → ε

where A, D 1 ,....,D n are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − If the start symbol S occurs on some right side, create a new start symbol S' and a new production S' → S .

Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)

Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)

Step 4 − Remove all direct and indirect left-recursion.

Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.

Masalah

Convert the following CFG into CNF

S → XY | Xn | hal

X → mX | m

Y → Xn | Hai

Larutan

Here, S does not appear on the right side of any production and there are no unit or null productions in the production rule set. So, we can skip Step 1 to Step 3.

Langkah 4

Now after replacing

X in S → XY | Xo | hal

dengan

mX | m

kami memperoleh

S → mXY | mY | mXo | mo | hal.

And after replacing

X in Y → X n | Hai

with the right side of

X → mX | m

kami memperoleh

Y → mXn | mn | Hai.

Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −

S → mXY | mY | mXC | mC | hal

X → mX | m

Y → mXD | mD | Hai

O → o

P → p

Pumping Lemma for CFG

Lemma

If L is a context-free language, there is a pumping length p such that any string w ∈ L of length ≥ p can be written as w = uvxyz , where vy ≠ ε , |vxy| ≤ p , and for all i ≥ 0, uv i xy i z ∈ L .

Applications of Pumping Lemma

Pumping lemma is used to check whether a grammar is context free or not. Let us take an example and show how it is checked.

Masalah

Find out whether the language L = {x n y n z n | n ≥ 1} is context free or not.

Larutan

Let L is context free. Then, L must satisfy pumping lemma.

At first, choose a number n of the pumping lemma. Then, take z as 0 n 1 n 2 n .

Break z into uvwxy, where

|vwx| ≤ n and vx ≠ ε.

Hence vwx cannot involve both 0s and 2s, since the last 0 and the first 2 are at least (n+1) positions apart. There are two cases −

Case 1 − vwx has no 2s. Then vx has only 0s and 1s. Then uwy , which would have to be in L , has n 2s, but fewer than n 0s or 1s.

Case 2 − vwx has no 0s.

Here contradiction occurs.

Hence, L is not a context-free language.

Pushdown Automata Introduction

Basic Structure of PDA

A pushdown automaton is a way to implement a context-free grammar in a similar way we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

Basically a pushdown automaton is −

"Finite state machine" + "a stack"

A pushdown automaton has three components −

• an input tape,
• a control unit, and
• a stack with infinite size.

The stack head scans the top symbol of the stack.

A stack does two operations −

• Push − a new symbol is added at the top.
• Pop − the top symbol is read and removed.

A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.

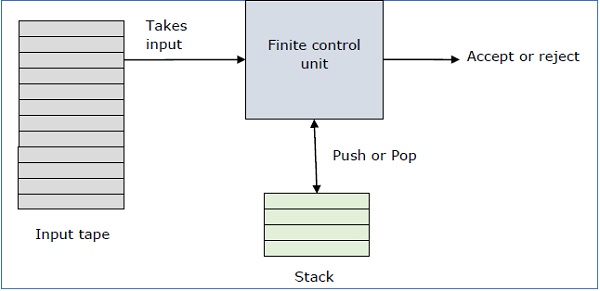
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0 , I, F) −

• Q is the finite number of states
• ∑ is input alphabet
• S is stack symbols
• δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*
• q 0 is the initial state (q 0 ∈ Q)
• I is the initial stack top symbol (I ∈ S)
• F is a set of accepting states (F ∈ Q)

Diagram berikut menunjukkan transisi dalam PDA dari keadaan q 1 ke keadaan q 2 , dilabeli sebagai a, b → c -

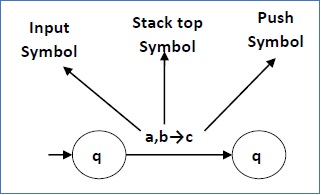
Ini berarti pada status q 1 , jika kita menemukan string input 'a' dan simbol atas stack adalah 'b' , maka kita pop 'b' , tekan 'c' di atas stack dan pindah ke status q 2 .

Terminologi Terkait dengan PDA

Deskripsi sesaat

Deskripsi instan (ID) PDA diwakili oleh triplet (q, w, s) di mana

• q adalah negara
• w adalah input yang tidak digunakan
• s adalah isi stack

Notasi Turnstile

Notasi "turnstile" digunakan untuk menghubungkan pasangan ID yang mewakili satu atau banyak gerakan PDA. Proses transisi dilambangkan dengan simbol pintu putar "⊢".

Pertimbangkan PDA (Q,, S, δ, q 0 , I, F). Transisi dapat secara matematis diwakili oleh notasi turnstile berikut -

(p, aw, Tβ) ⊢ (q, w, αb)

Ini menyiratkan bahwa saat mengambil transisi dari keadaan p ke keadaan q , simbol input 'a' dikonsumsi, dan bagian atas tumpukan 'T' diganti oleh string baru 'α' .

Catatan - Jika kita menginginkan nol atau lebih gerakan dari PDA, kita harus menggunakan simbol (⊢ *) untuk itu.

Penerimaan Pushdown Automata

Ada dua cara berbeda untuk mendefinisikan penerimaan PDA.

Penerimaan Keadaan Akhir

Dalam keadaan penerimaan terakhir, PDA menerima string ketika, setelah membaca seluruh string, PDA berada dalam keadaan akhir. Dari kondisi awal, kita dapat membuat gerakan yang berakhir pada kondisi akhir dengan nilai stack apa pun. Nilai tumpukan tidak relevan selama kita berakhir dalam keadaan akhir.

Untuk PDA (Q, ∑, S, δ, q 0 , I, F), bahasa yang diterima oleh himpunan status akhir F adalah -

L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}

untuk setiap string tumpukan input x .

Penerimaan Stack Kosong

Di sini PDA menerima string ketika, setelah membaca seluruh string, PDA telah mengosongkan tumpukannya.

For a PDA (Q, ∑, S, δ, q 0 , I, F), the language accepted by the empty stack is −

L(PDA) = {w | (q 0 , w, I) ⊢* (q, ε, ε), q ∈ Q}

Contoh

Construct a PDA that accepts L = {0 n 1 n | n ≥ 0}

Larutan

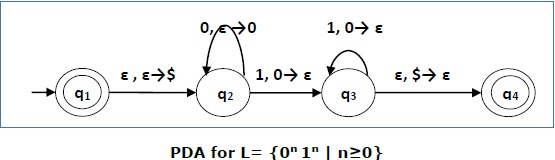
This language accepts L = {ε, 01, 0011, 000111, ............................. }

Here, in this example, the number of 'a' and 'b' have to be same.

• Initially we put a special symbol '$' into the empty stack.
• Then at state q 2 , if we encounter input 0 and top is Null, we push 0 into stack. This may iterate. And if we encounter input 1 and top is 0, we pop this 0.
• Then at state q 3 , if we encounter input 1 and top is 0, we pop this 0. This may also iterate. And if we encounter input 1 and top is 0, we pop the top element.
• If the special symbol '$' is encountered at top of the stack, it is popped out and it finally goes to the accepting state q 4 .

Contoh

Construct a PDA that accepts L = { ww R | w = (a+b)* }

Larutan

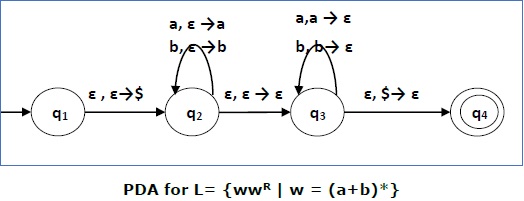
Initially we put a special symbol '$' into the empty stack. At state q 2 , the w is being read. In state q 3 , each 0 or 1 is popped when it matches the input. If any other input is given, the PDA will go to a dead state. When we reach that special symbol '$', we go to the accepting state q 4 .

PDA & Context-Free Grammar

If a grammar G is context-free, we can build an equivalent nondeterministic PDA which accepts the language that is produced by the context-free grammar G . A parser can be built for the grammar G .

Also, if P is a pushdown automaton, an equivalent context-free grammar G can be constructed where

L(G) = L(P)

In the next two topics, we will discuss how to convert from PDA to CFG and vice versa.

Algorithm to find PDA corresponding to a given CFG

Input − A CFG, G = (V, T, P, S)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q 0 , I, F)

Step 1 − Convert the productions of the CFG into GNF.

Step 2 − The PDA will have only one state {q}.

Step 3 − The start symbol of CFG will be the start symbol in the PDA.

Step 4 − All non-terminals of the CFG will be the stack symbols of the PDA and all the terminals of the CFG will be the input symbols of the PDA.

Step 5 − For each production in the form A → aX where a is terminal and A, X are combination of terminal and non-terminals, make a transition δ (q, a, A) .

Masalah

Construct a PDA from the following CFG.

G = ({S, X}, {a, b}, P, S)

where the productions are −

S → XS | ε , A → aXb | Ab | ab

Larutan

Let the equivalent PDA,

P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)

where δ −

δ(q, ε , S) = {(q, XS), (q, ε )}

δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}

δ(q, a, a) = {(q, ε )}

δ(q, 1, 1) = {(q, ε )}

Algorithm to find CFG corresponding to a given PDA

Input − A CFG, G = (V, T, P, S)

Output - PDA Setara, P = (Q,, S, δ, q 0 , I, F) sedemikian rupa sehingga non-terminal dari tata bahasa G akan menjadi {X wx | w, x ∈ Q} dan negara mulai akan A q0, F .

Langkah 1 - Untuk setiap w, x, y, z ∈ Q, m ∈ S dan a, b ∈ β, jika δ (w, a, ε) berisi (y, m) dan (z, b, m) berisi ( x, ε), tambahkan aturan produksi X wx → a X yz b dalam tata bahasa G.

Langkah 2 - Untuk setiap w, x, y, z ∈ Q, tambahkan aturan produksi X wx → X wy X yx dalam tata bahasa G.

Langkah 3 - Untuk w ∈ Q, tambahkan aturan produksi X ww → ε dalam tata bahasa G.

Automdown & Parsing

Parsing digunakan untuk mendapatkan string menggunakan aturan produksi tata bahasa. Ini digunakan untuk memeriksa penerimaan string. Compiler digunakan untuk memeriksa apakah string benar secara sintaksis atau tidak. Pengurai mengambil input dan membangun pohon pengurai.

Parser dapat terdiri dari dua jenis -

• Parser Top-Down - penguraian Top-down dimulai dari atas dengan simbol awal dan memperoleh string menggunakan pohon parse.
• Bottom-Up Parser - Parsing bottom-up dimulai dari bawah dengan string dan datang ke simbol awal menggunakan pohon parse.

Desain Top-Down Parser

Untuk penguraian top-down, PDA memiliki empat jenis transisi berikut -

• Pop non-terminal di sisi kiri produksi di bagian atas tumpukan dan dorong tali sisi kanannya.
• Jika simbol teratas tumpukan sesuai dengan simbol input yang sedang dibaca, letakan.
• Dorong simbol awal 'S' ke dalam tumpukan.
• Jika string input sepenuhnya dibaca dan tumpukan kosong, lanjutkan ke status akhir 'F'.

Contoh

Desain parser top-down untuk ekspresi "x + y * z" untuk tata bahasa G dengan aturan produksi berikut -

P: S → S + X | X, X → X * Y | Y, Y → (S) | Indo

Larutan

Jika PDA adalah (Q, ∑, S, δ, q 0 , I, F), maka penguraian top-down adalah -

(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)

⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)

⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)

Desain Parser Bottom-Up

Untuk penguraian bottom-up, PDA memiliki empat jenis transisi berikut -

• Dorong simbol input saat ini ke tumpukan.
• Ganti sisi kanan produksi di bagian atas tumpukan dengan sisi kiri.
• Jika bagian atas elemen tumpukan cocok dengan simbol input saat ini, letakan itu.
• Jika string input sepenuhnya dibaca dan hanya jika simbol awal 'S' tetap di tumpukan, pop dan pergi ke keadaan akhir 'F'.

Contoh

Desain parser top-down untuk ekspresi "x + y * z" untuk tata bahasa G dengan aturan produksi berikut -

P: S → S + X | X, X → X * Y | Y, Y → (S) | Indo

Larutan

Jika PDA adalah (Q, ∑, S, δ, q 0 , I, F), maka penguraian bottom-up adalah -

(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)

⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)

⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)

Pendahuluan Mesin Turing

Mesin Turing adalah perangkat penerima yang menerima bahasa (himpunan enumerable berulang) yang dihasilkan oleh tata bahasa tipe 0. Itu ditemukan pada tahun 1936 oleh Alan Turing.

Definisi

Turing Machine (TM) adalah model matematika yang terdiri dari pita panjang tak terbatas dibagi menjadi sel-sel di mana input diberikan. Terdiri dari kepala yang membaca rekaman input. Register negara menyimpan status mesin Turing. Setelah membaca simbol input, ia diganti dengan simbol lain, keadaan internalnya diubah, dan bergerak dari satu sel ke kanan atau kiri. Jika TM mencapai kondisi akhir, string input diterima, jika tidak ditolak.

TM dapat secara formal digambarkan sebagai 7-tupel (Q, X, ∑, δ, q 0 , B, F) di mana -

• Q adalah seperangkat status terbatas
• X adalah alfabet rekaman
• ∑ adalah alfabet input
• δ adalah fungsi transisi; δ: Q × X → Q × X × {Left_shift, Right_shift}.
• q 0 adalah kondisi awal
• B adalah simbol kosong
• F adalah himpunan status akhir

Perbandingan dengan otomat sebelumnya

Tabel berikut menunjukkan perbandingan bagaimana mesin Turing berbeda dari Finite Automaton dan Pushdown Automaton.

Mesin	Struktur Data Stack	Deterministik?
Hingga otomat	NA	Iya
Automat Pushdown	Last In First Out (LIFO)	Tidak
Mesin Turing	Rekaman tak terbatas	Iya

Contoh mesin Turing

Mesin Turing M = (Q, X, ∑, δ, q 0 , B, F) dengan

• Q = {q 0 , q 1 , q 2 , q f }
• X = {a, b}
• Β = {1}
• q 0 = {q 0 }
• B = simbol kosong
• F = {q f }

δ diberikan oleh -

Pita simbol alfabet	Status Saat Ini 'q 0 '	Status Saat Ini 'q 1 '	Status Saat Ini 'q 2 '
Sebuah	1Rq 1	1 Lq 0	1Lq f
b	1Lq 2	1Rq 1	1Rq f

Di sini transisi 1Rq 1 menyiratkan bahwa simbol tulis adalah 1, rekaman bergerak ke kanan, dan negara berikutnya adalah q 1 . Demikian pula, transisi 1Lq 2 menyiratkan bahwa simbol tulis adalah 1, rekaman bergerak ke kiri, dan negara berikutnya adalah q 2 .

Time and Space Complexity of a Turing Machine

For a Turing machine, the time complexity refers to the measure of the number of times the tape moves when the machine is initialized for some input symbols and the space complexity is the number of cells of the tape written.

Time complexity all reasonable functions −

T(n) = O(n log n)

TM's space complexity −

S(n) = O(n)

Accepted Language & Decided Language

A TM accepts a language if it enters into a final state for any input string w. A language is recursively enumerable (generated by Type-0 grammar) if it is accepted by a Turing machine.

A TM decides a language if it accepts it and enters into a rejecting state for any input not in the language. A language is recursive if it is decided by a Turing machine.

There may be some cases where a TM does not stop. Such TM accepts the language, but it does not decide it.

Designing a Turing Machine

The basic guidelines of designing a Turing machine have been explained below with the help of a couple of examples.

Contoh 1

Design a TM to recognize all strings consisting of an odd number of α's.

Solution

The Turing machine M can be constructed by the following moves −

• Let q 1 be the initial state.
• If M is in q 1 ; on scanning α, it enters the state q 2 and writes B (blank).
• If M is in q 2 ; on scanning α, it enters the state q 1 and writes B (blank).
• From the above moves, we can see that M enters the state q 1 if it scans an even number of α's, and it enters the state q 2 if it scans an odd number of α's. Hence q 2 is the only accepting state.

Karenanya,

M = {{q 1 , q 2 }, {1}, {1, B}, δ, q 1 , B, {q 2 }}

where δ is given by −

Tape alphabet symbol	Present State 'q 1 '	Present State 'q 2 '
α	BRq 2	BRq 1

Contoh 2

Design a Turing Machine that reads a string representing a binary number and erases all leading 0's in the string. However, if the string comprises of only 0's, it keeps one 0.

Solution

Let us assume that the input string is terminated by a blank symbol, B, at each end of the string.

The Turing Machine, M , can be constructed by the following moves −

• Let q 0 be the initial state.
• If M is in q 0 , on reading 0, it moves right, enters the state q 1 and erases 0. On reading 1, it enters the state q 2 and moves right.
• If M is in q 1 , on reading 0, it moves right and erases 0, ie, it replaces 0's by B's. On reaching the leftmost 1, it enters q 2 and moves right. If it reaches B, ie, the string comprises of only 0's, it moves left and enters the state q 3 .
• If M is in q 2 , on reading either 0 or 1, it moves right. On reaching B, it moves left and enters the state q 4 . This validates that the string comprises only of 0's and 1's.
• If M is in q 3 , it replaces B by 0, moves left and reaches the final state q f .
• If M is in q 4 , on reading either 0 or 1, it moves left. On reaching the beginning of the string, ie, when it reads B, it reaches the final state q f .

Karenanya,

M = {{q 0 , q 1 , q 2 , q 3 , q 4 , q f }, {0,1, B}, {1, B}, δ, q 0 , B, {q f }}

where δ is given by −

Tape alphabet symbol	Present State 'q 0 '	Present State 'q 1 '	Present State 'q 2 '	Present State 'q 3 '	Present State 'q 4 '
0	BRq 1	BRq 1	ORq 2	-	OLq 4
1	1Rq 2	1Rq 2	1Rq 2	-	1Lq 4
B	BRq 1	BLq 3	BLq 4	OLq f	BRQ f

Mesin Turing Multi-tape

Mesin Turing Multi-tape memiliki beberapa kaset di mana setiap kaset diakses dengan kepala yang terpisah. Setiap kepala dapat bergerak secara independen dari kepala lainnya. Awalnya input ada di tape 1 dan yang lainnya kosong. Pada awalnya, kaset pertama ditempati oleh input dan kaset lainnya disimpan kosong. Selanjutnya, mesin membaca simbol berturut-turut di bawah kepalanya dan TM mencetak simbol pada setiap pita dan menggerakkan kepalanya.

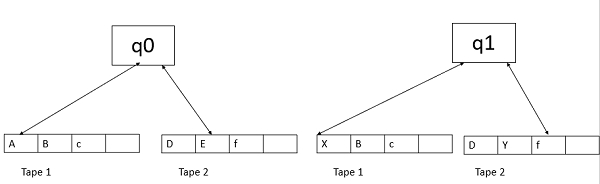
Mesin Multi-tape Turing dapat secara resmi digambarkan sebagai 6-tupel (Q, X, B, δ, q 0 , F) di mana -

• Q adalah seperangkat status terbatas
• X adalah alfabet rekaman
• B adalah simbol kosong
• δ adalah relasi pada status dan simbol di mana
  δ: Q × X k → Q × (X × {Left_shift, Right_shift, No_shift}) k
  di mana ada jumlah k kaset
• q 0 adalah kondisi awal
• F adalah himpunan status akhir

Catatan - Setiap mesin Multi-tape Turing memiliki mesin Turing single-tape yang setara.

Mesin Turing Multi-track

Mesin Multi-track Turing, tipe spesifik dari mesin Multi-tape Turing, berisi banyak track tetapi hanya satu head tape yang membaca dan menulis di semua track. Di sini, kepala kaset tunggal membaca n simbol dari n trek pada satu langkah. Ini menerima bahasa enumerable rekursif seperti yang diterima Turing Machine single-tape single-track normal.

Mesin Multi-track Turing dapat secara formal digambarkan sebagai 6-tupel (Q, X, ∑, δ, q 0 , F) di mana -

• Q adalah seperangkat status terbatas
• X adalah alfabet rekaman
• ∑ adalah alfabet input
• δ adalah relasi pada status dan simbol di mana
  δ (Q i , [a 1 , a 2 , 3 , ....]) = (Q j , [b 1 , b 2 , b 3 , ....], Left_shift atau Right_shift)
• q 0 adalah kondisi awal
• F adalah himpunan status akhir

Catatan - Untuk setiap Turing Machine single-track S , ada Turing Machine multi-track M yang setara sehingga L (S) = L (M) .

Mesin Turing Non-deterministik

Dalam Mesin Turing Non-Deterministik, untuk setiap negara dan simbol, ada sekelompok tindakan yang dapat dilakukan TM. Jadi, di sini transisinya tidak deterministik. Perhitungan Mesin Turing non-deterministik adalah pohon konfigurasi yang dapat dicapai dari konfigurasi awal.

Input diterima jika setidaknya ada satu simpul dari pohon yang merupakan konfigurasi terima, jika tidak maka tidak akan diterima. Jika semua cabang dari pohon komputasi berhenti pada semua input, Mesin Turing non-deterministik disebut Penentu dan jika untuk beberapa input, semua cabang ditolak, input juga ditolak.

Mesin Turing non-deterministik dapat secara resmi didefinisikan sebagai 6-tupel (Q, X,, δ, q 0 , B, F) di mana -

• Q adalah seperangkat status terbatas
• X adalah alfabet rekaman
• ∑ adalah alfabet input
• δ adalah fungsi transisi;
  δ: Q × X → P (Q × X × {Left_shift, Right_shift}).
• q 0 adalah kondisi awal
• B adalah simbol kosong
• F adalah himpunan status akhir

Mesin Pita Turing Semi-Tak Terbatas

Mesin Turing dengan pita semi-tak terbatas memiliki ujung kiri tetapi tanpa ujung kanan. Ujung kiri terbatas dengan penanda ujung.

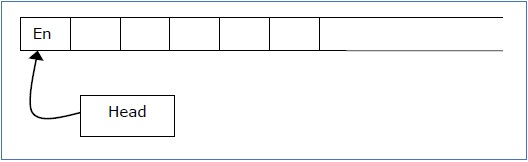
Ini adalah rekaman dua jalur -

• Jalur atas - Ini mewakili sel di sebelah kanan posisi kepala awal.
• Jalur bawah - Ini mewakili sel-sel di sebelah kiri posisi kepala awal dalam urutan terbalik.

String masukan panjang tak terbatas pada awalnya ditulis pada pita dalam sel-sel pita yang berdekatan.

Mesin mulai dari keadaan awal q 0 dan kepala memindai dari ujung kiri 'End'. Di setiap langkah, ia membaca simbol pada pita di bawah kepalanya. Itu menulis simbol baru pada sel rekaman itu dan kemudian memindahkan kepala baik ke kiri atau ke kanan satu sel pita. Fungsi transisi menentukan tindakan yang harus diambil.

Ia memiliki dua negara khusus yang disebut menerima negara dan menolak negara . Jika suatu saat memasuki keadaan diterima, input diterima dan jika masuk ke kondisi tolak, input ditolak oleh TM. Dalam beberapa kasus, ini terus berjalan tanpa batas tanpa diterima atau ditolak untuk beberapa simbol input tertentu.

Catatan - Mesin Turing dengan pita semi-tak terbatas setara dengan mesin Turing standar.

Automata Terikat Linier

Automaton terikat linier adalah mesin Turing non-deterministik multi-track dengan pita beberapa panjang terbatas terbatas.

Panjang = fungsi (Panjang string input awal, konstan c)

Sini,

Informasi memori ≤ c × Informasi input

Perhitungan dibatasi pada area yang dibatasi konstan. Alfabet input berisi dua simbol khusus yang berfungsi sebagai spidol ujung kiri dan spidol ujung kanan yang berarti transisi tidak bergerak ke kiri dari penanda ujung kiri atau ke kanan penanda ujung kanan rekaman.

Otomat yang dibatasi linear dapat didefinisikan sebagai 8-tupel (Q, X, ∑, q 0 , ML, MR, δ, F) di mana -

• Q adalah seperangkat status terbatas
• X adalah alfabet rekaman
• ∑ adalah alfabet input
• q 0 adalah kondisi awal
• M L adalah penanda ujung kiri
• M R adalah penanda ujung kanan di mana M R ≠ M L
• δ adalah fungsi transisi yang memetakan setiap pasangan (negara, simbol pita) ke (negara, simbol pita, Konstan 'c') di mana c dapat berupa 0 atau +1 atau -1
• F adalah himpunan status akhir

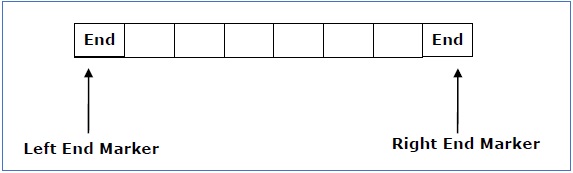
Otomat terikat linear deterministik selalu peka konteks dan otomat terikat linier dengan bahasa kosong tidak dapat ditentukan . .

Decidability Bahasa

Suatu bahasa disebut Decidable atau Recursive jika ada mesin Turing yang menerima dan berhenti pada setiap string input w . Setiap bahasa yang dapat memutuskan adalah Turing-Acceptable.

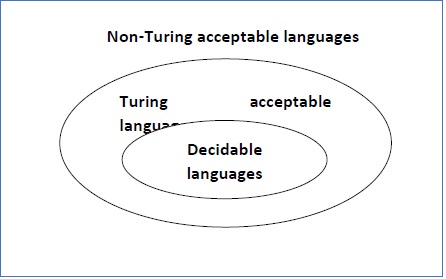
Masalah keputusan P dapat diputuskan jika bahasa L dari semua instance ya ke P dapat ditentukan.

Untuk bahasa yang dapat ditentukan, untuk setiap string input, TM berhenti pada status accept atau reject seperti yang digambarkan dalam diagram berikut -

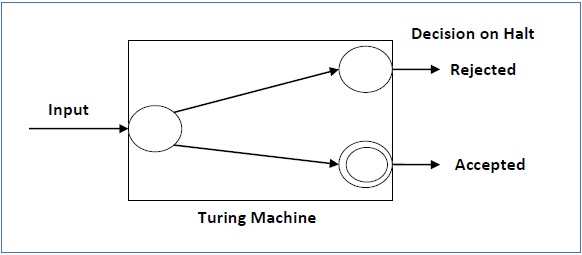
Contoh 1

Cari tahu apakah masalah berikut ini dapat ditentukan atau tidak -

Apakah angka 'm' prima?

Larutan

Bilangan prima = {2, 3, 5, 7, 11, 13, ………… ..}

Bagilah angka 'm' dengan semua angka antara '2' dan '√m' mulai dari '2'.

Jika salah satu dari angka-angka ini menghasilkan sisa nol, maka itu pergi ke "Keadaan ditolak", jika tidak pergi ke "Keadaan yang diterima". Jadi, di sini jawabannya bisa dibuat dengan 'Ya' atau 'Tidak'.

Oleh karena itu, ini merupakan masalah yang dapat diperhitungkan.

Contoh 2

Diberi bahasa reguler L dan string w , bagaimana kita bisa memeriksa apakah w ∈ L ?

Larutan

Ambil DFA yang menerima L dan periksa apakah w diterima

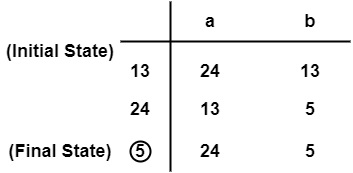
Beberapa masalah yang lebih baik adalah -

• Apakah DFA menerima bahasa kosong?
• Apakah L 1 ∩ L 2 = ∅ untuk set reguler?

Catatan -

• Jika suatu bahasa L dapat dipilih, maka komplemen L ' juga dapat ditentukan
• Jika suatu bahasa dapat dipilih, maka ada enumerator untuk itu.

Bahasa yang Tidak Diputuskan

Untuk bahasa yang tidak dapat ditentukan, tidak ada Mesin Turing yang menerima bahasa dan membuat keputusan untuk setiap string input w (TM dapat membuat keputusan untuk beberapa string input). Masalah keputusan P disebut "tidak dapat dipastikan" jika bahasa L dari semua contoh ya untuk P tidak dapat ditentukan. Bahasa yang tidak dapat ditentukan bukan bahasa rekursif, tetapi kadang-kadang, mereka mungkin bahasa yang dihitung secara rekursif.

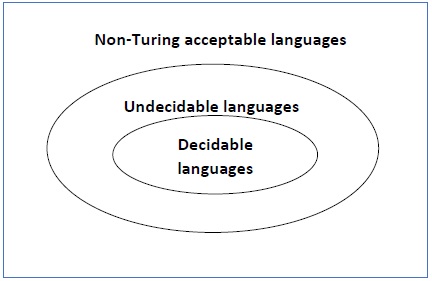
Contoh

• Masalah berhentinya mesin Turing
• Masalah kematian
• Masalah matriks fana
• Masalah surat menyurat, dll.

Mesin Turing Menghentikan Masalah

Input - Mesin Turing dan string input w .

Soal - Apakah Turing mesin finish komputasi dari string w dalam jumlah terbatas langkah? Jawabannya harus ya atau tidak.

Bukti - Pada awalnya, kami akan menganggap bahwa mesin Turing seperti ada untuk menyelesaikan masalah ini dan kemudian kami akan menunjukkan itu bertentangan dengan dirinya sendiri. Kami akan menyebut mesin Turing ini sebagai mesin Berhenti yang menghasilkan 'ya' atau 'tidak' dalam jumlah waktu yang terbatas. Jika mesin penghenti selesai dalam jumlah waktu yang terbatas, hasilnya berupa 'ya', atau 'tidak'. Berikut ini adalah diagram blok dari mesin Halting -

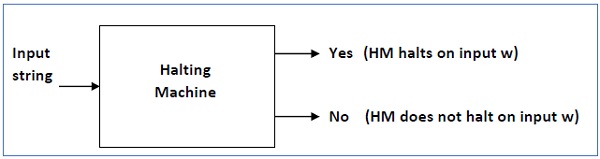
Sekarang kita akan merancang mesin penghentian terbalik (HM) ' sebagai -

• Jika H mengembalikan YA, maka ulangi selamanya.
• Jika H mengembalikan TIDAK, maka berhentilah.

Berikut ini adalah diagram blok 'Mesin penghenti terbalik' -

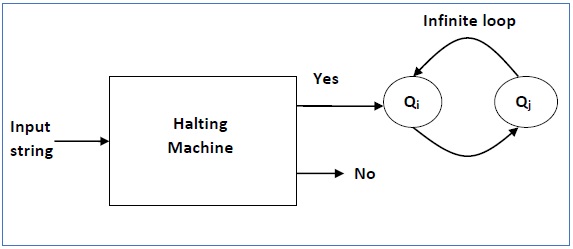
Selanjutnya, sebuah mesin (HM) 2 yang inputnya dibangun sebagai berikut -

• Jika (HM) 2 berhenti pada input, ulangi selamanya.
• Lain, berhenti.

Di sini, kita punya kontradiksi. Oleh karena itu, masalah penghentian tidak dapat diputuskan .

Teorema Padi

Teorema Padi menyatakan bahwa setiap properti semantik non-sepele dari suatu bahasa yang dikenali oleh mesin Turing tidak dapat diputuskan. Properti, P, adalah bahasa dari semua mesin Turing yang memuaskan properti itu.

Definisi Resmi

Jika P adalah properti non-sepele, dan bahasa yang memegang properti, Lp , dikenali oleh mesin Turing M, maka L p = {<M> | L (M) ∈ P} tidak dapat ditentukan.

Deskripsi dan Properti

• Properti bahasa, P, hanyalah seperangkat bahasa. Jika bahasa apa pun milik P (L ∈ P), dikatakan bahwa L memenuhi properti P.
• Properti disebut sepele jika tidak puas dengan bahasa enumerable rekursif, atau jika dipenuhi oleh semua bahasa enumerable rekursif.
• Properti non-sepele dipenuhi oleh beberapa bahasa yang berulang secara berulang dan tidak puas oleh yang lain. Secara formal, di properti non-sepele, di mana L ∈ P, keduanya memiliki properti berikut:
  • Properti 1 - Terdapat Mesin Turing, M1 dan M2 yang mengenali bahasa yang sama, yaitu (<M1>, <M2> ∈ L) atau (<M1>, <M2> ∉ L)
  • Properti 2 - Terdapat Mesin Turing M1 dan M2, di mana M1 mengenali bahasa sementara M2 tidak, yaitu <M1> ∈ L dan <M2> ∉ L

Bukti

Misalkan, properti P adalah non-sepele dan φ ∈ P.

Karena, P adalah non-sepele, setidaknya satu bahasa memenuhi P, yaitu, L (M 0 ) ∈ P, ∋ Mesin Turing M 0 .

Biarkan, w menjadi input dalam instan tertentu dan N adalah Mesin Turing yang mengikuti -

Pada input x

• Jalankan M pada w
• Jika M tidak menerima (atau tidak berhenti), maka jangan terima x (atau jangan berhenti)
• Jika M menerima w maka jalankan M 0 pada x. Jika M 0 menerima x, maka menerima x.

Fungsi yang memetakan instance ATM = {<M, w> | M menerima input w} ke N sehingga

• Jika M menerima w dan N menerima bahasa yang sama dengan M 0 , Maka L (M) = L (M 0 ) ∈ p
• Jika M tidak menerima w dan N menerima φ, Maka L (N) = φ ∉ hlm

Karena A TM tidak dapat ditentukan dan dapat dikurangi menjadi Lp, Lp juga tidak dapat ditentukan.

Pasca Korespondensi Masalah

Post Correspondence Problem (PCP), yang diperkenalkan oleh Emil Post pada tahun 1946, adalah masalah keputusan yang tidak dapat diputuskan. Masalah PCP atas alfabet β dinyatakan sebagai berikut -

Diberikan dua daftar berikut, M dan N string tidak kosong di atas ∑ -

M = (x 1 , x 2 , x 3 , ………, x n )

N = (y 1 , y 2 , y 3 , ………, y n )

Kita dapat mengatakan bahwa ada Solusi Post Correspondence, jika untuk beberapa i 1 , i 2 , ………… i k , di mana 1 ≤ i j ≤ n, kondisi x i1 …… .x ik = y i1 ……. y ik memenuhi.

Contoh 1

Temukan apakah daftarnya

M = (abb, aa, aaa) dan N = (bba, aaa, aa)

punya Solusi Post Correspondence?

Larutan

	x 1	x 2	x 3
M.	Abb	A A	aaa
N	Bba	aaa	A A

Sini,

x 2 x 1 x 3 = 'aaabbaaa'

dan y 2 y 1 y 3 = 'aaabbaaa'

Kita bisa melihatnya

x 2 x 1 x 3 = y 2 y 1 y 3

Oleh karena itu, solusinya adalah i = 2, j = 1, dan k = 3.

Contoh 2

Cari apakah daftar M = (ab, bab, bbaaa) dan N = (a, ba, bab) memiliki Solusi Post Correspondence?

Larutan

	x 1	x 2	x 3
M.	ab	bab	bbaaa
N	Sebuah	ba	bab

Dalam hal ini, tidak ada solusi karena -

| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Panjangnya tidak sama)

Oleh karena itu, dapat dikatakan bahwa Masalah Post Correspondence ini tidak dapat dipastikan .

Daftar Pustaka :

1. https://www.geeksforgeeks.org/lmn-toc/

2. https://www.tutorialspoint.com/automata_theory/automata_theory_quick_guide.htm